【数学　無敵の勉強法】「数学は方法です。才能じゃない」

　

東進のカリスマ講師「苑田尚之」さんの名言。

「数式は言葉です。計算じゃない。」

　

この動画の0:07～0:10の３秒間ですが、非常に好きです。大好きですｗ

ということで、

タイトルで少し文字らせていただきました。

　

はい。

お遊びはこのくらいにして、本題入ります。今回は

数学の勉強法

について紹介します。誰でも数学はできるようになります。やり方さえ正しければ、必ず成果は出ます。

ぜひ今回数学の勉強法の神髄を見ていってください。

　

数学の勉強法　数学に必要なもの

まず数学に必要なものって何だと思いますか。

　

　

ヒラメキ、思考力、柔軟さ…

　

　

確かにあった方が有利なのは事実です。でも大学受験の数学において重要なのは、

　

・覚えた解法

・翻訳能力

・計算力

　

この３つがあれば、東大でも楽々受かります。どんなに弱いおつむを持っていても、上の３つを揃えれば余裕なんです。

　

①覚えた解法

これは私が「解法」について話すときに使う話なんですが、

最近の「定期テスト」と「教科書＆問題集」を持ってきてください。教科書と問題集は試験範囲のものです。

　

試しに定期テストで間違えた問題を探してみましょう。

この問題どこかで見たことありませんか。

教科書か問題集に載っていた気がしませんか。

　

真面目に勉強してきた人ほど分かりますよね。

　

定期テストの問題は９９％の確率で、同じor数字変えの問題が「教科書＆問題集」に載っています。

超進学校でも５０％くらいはそうです。

　

同じことは大学受験でも高校受験でも起こります。定期テスト＝「入試」で、教科書＆問題集＝「参考書」だと思ってください。

　

世の中どんな大学でも、たいていの入試問題は参考書の数字変え。悪くても類題です。

東大の問題ですら、青チャートに類題がチラホラ。センター試験なんてどの問題も参考書に類題が載っています。

　

しかも大学受験数学は今ネタ切れ状態。

これからはより典型問題ばかりが入試問題に出て、参考書をやって解法パターンをたくさん知っている人が強い時代になるのではないかと思います。

　

「数学で偏差値７０超える人ってさぞかしヒラメキ力が高いんだろうな～」みたいに思っていた人。

数学なんて結局、どれだけのパターンを使いこなせるか。

　

成績優秀者の中で、試験中に１から考えて問題を解いているような人なんていません。

模試なんかは特に、試験中はただひたすら知っている解法に当てはめて手を動かすだけ。

私も東進のセンター模試なんかを解いているときは一切脳は機能してないです。ただ計算するだけ。

　

②翻訳能力

数式は言葉なんですよねｗ

　

「判別式＞０」＝「２次方程式が異なる２解を持つ」

「y＝f(x)が（2,5）を通る」＝「5＝f(2)を満たす」

　

みたいに日本語と数式の条件を行ったり来たり出来る人は数学が強いですよね。

問題文から数式に落とし込めれば、必ず解けるようにできてますから。

　

「なんだ結局才能かよ。俺には無理だ」

　

とか思わないでください。

これも私の推奨する勉強法で参考書をやっていけば、ごく自然に身についていく力です。

むしろ特定の日本語が出てきたら数式に直さずには先を読めなくなります。

　

もはや病気。

「f(x)が（1,4）で接線…」→「はい。f(x)微分してx=1代入」

そんな感じです。

　

結局はパターンを身に着けていく中で養える力です。

ただの慣れ。

　

③正確な計算力

解き方は分かったけど、計算ミスで×。

あとちょっとで解けそうだったのに、計算が遅くて×。

　

数学は嫌でも計算しなければ答えが出ません。そして、計算を間違えてしまえば今までの過程は無になります。

計算が遅ければセンター数学のような膨大な量を消化することは難しいです。

　

計算力は数学のかなめ。

　

「じゃあだめだよ。俺は計算遅いから数学ムリだわ」

　

　

とか言わないでｗ

これも解法パターン習得の過程でしっかり克服できます。

圧倒的に計算が楽になる方法だって参考書には載っているので、それごとマスターしちゃいましょう。

数学の勉強法　よくあるNG集

①悩んでたら１時間すぎてた…

よくあるのが、分からない問題に出会ったときに自力で何とかしようと悩んでいたら時間が過ぎてしまうパターン。

結果として、時間と精神を浪費しただけ。

　

それならサッサと答えを見てしまえばいいんです。

「下手の考え休むに似たり」

　

アホが考えても何も変わりません。入試本番のときに、その問題が解ければいい。

問題解いていて分からなかったら、心の中でこう思ってください。

「この問題は難しい…今はね。」

「今はね」を付けとけばカッコよく逃げられるんで、それでプライドは守ってくださいｗ

　

②１回解いてそのまま

出来ない問題をできるようにするから成長。

１回だけ解いて〇×つけても、自分の実力の確認をしただけで、何も成長してないです。

それこそ時間の無駄。

「お～。俺ってこんなに×多いだ」って思うために問題集やっているわけではないですよね。

　

「できない問題をできるように」、「今できる問題をより速く解けるように」と何度も解き直すのが正しい勉強法です。

　

③板書ガリガリマン

数学ほど板書が役に立たない教科はないかもしれません。

大切なことは全部教科書に書いてあります。

　

そして数学は人の話を聞いてもできるようになりません。自分の手を動かして勉強しないといつまでたっても出来ないまま。

授業は１人では理解が難しい内容を、人に解説してもらうことで理解するという意味しかないです。

　

だからわかる範囲の授業を聞くなんて、この世の最悪レベルで時間の無駄です。

　

「ノートに板書を取って見返すことで復習する。」と思っているのかもしれませんが、

いざ真っ白の問題を見たときに解けるかが大事なので、ヒントだらけのノートを見て復習するのは効果が薄いです。

　

そして参考書を買えば、ノートよりキレイに分かりやすくまとめてある解説がついています。

教科書にも解説がついています。

ノートを取る暇があれば、問題を１問でも多く解いては理解してを繰り返した方が圧倒的にいいです。

　

数学　無敵の勉強法

参考書の例題全暗記

　

途方もないように思えるかもしれませんが、問題を見た瞬間に解けるレベルになればいいので周回してればすぐできるようになります。

参考書を１冊完璧にすれば、見える景色は一気に変わります。

私も最初は54.6だった偏差値が

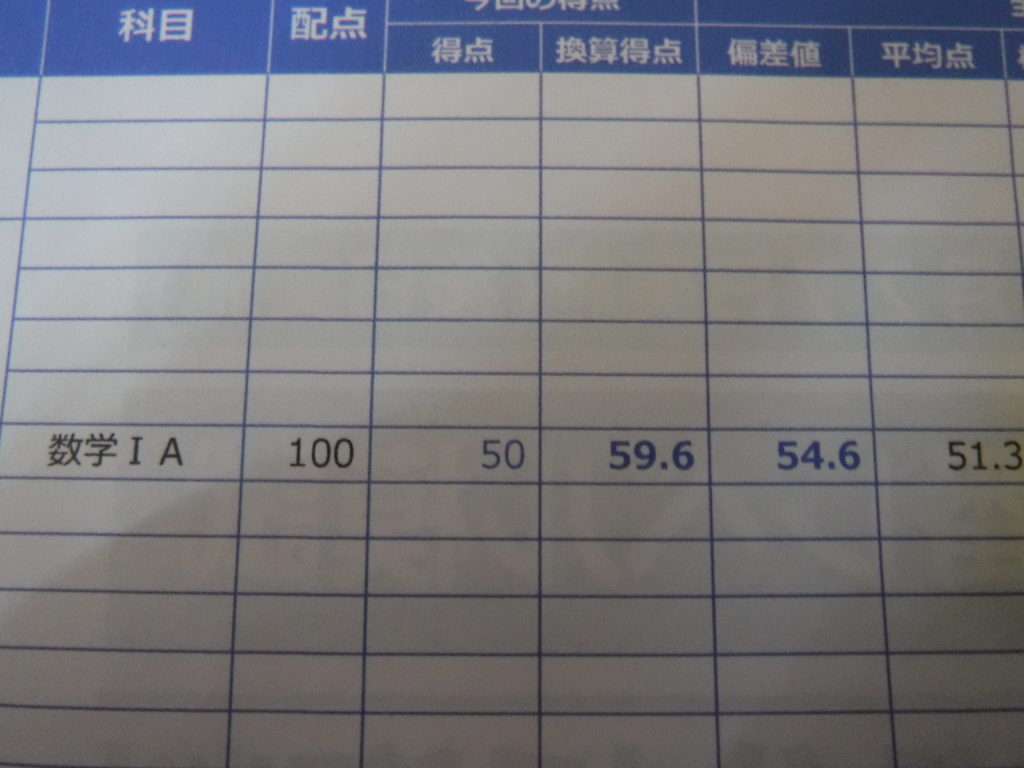
基礎問題精構という問題集１冊を３か月かけて完璧にしたら、

偏差値が

７０超えました

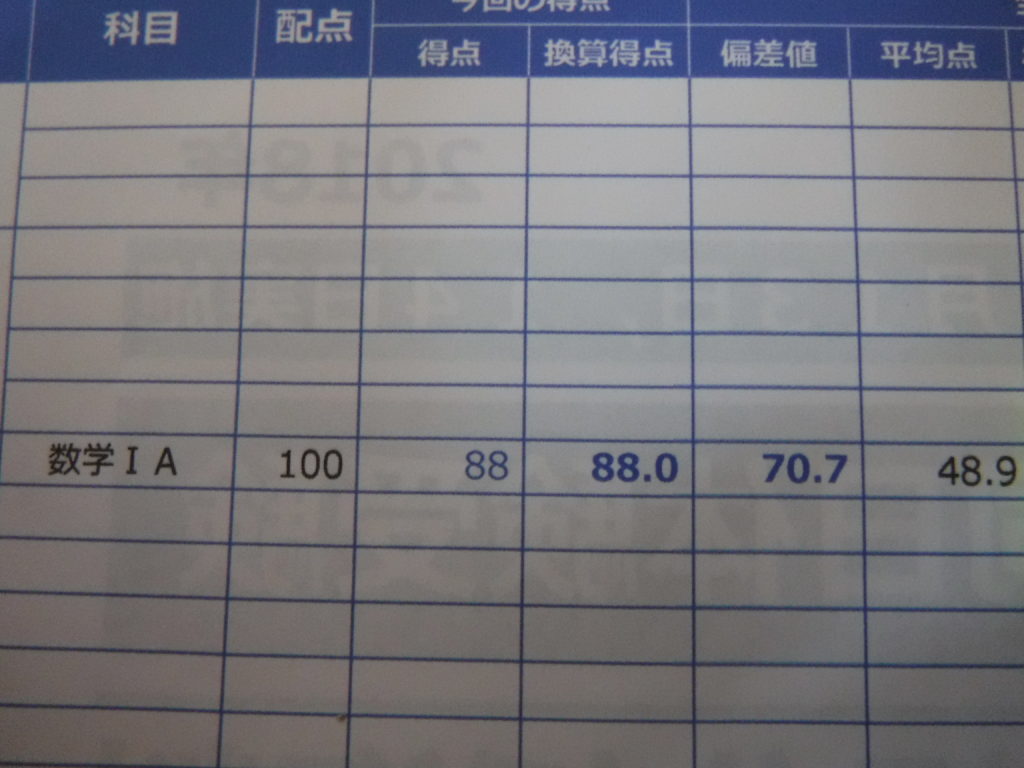
参考書を１冊極める＞＞＞何冊も手を出す

極めるっていうのは、基礎問題精構に書いてある問題をどんなものでも見た瞬間に解法が分かって、１分以内に答えが出せました。

そのレベルが極みです。

数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？

step1　解説を理解する

目安：１、２周

　

問題は解きません。

解説を読んで理解していきます。

どうしてこの方針なのか。なぜこの公式が使えるのか。

　

この問題には～～な特徴があるから〇〇の公式が有効だ。

　

などなど解説を完璧に理解して、問題に対する疑問点をすべてなくしていきます。

雑にやると後で丸暗記になってしまうので、じっくり理解。

　

step2　解法を習得する

目安：５周～７周

ひたすら問題を解いて、「あ～そうだった！」を繰り返します。

暗記しようとするのではなく、ただ無心で解き続けてください。間違えたら「あ～そうだった」で十分。

もう理解はしているので答え合わせもスムーズに進むはず。

　

解きまくってください。

毎日２０題くらい解けるんじゃないですか。５周目くらいになると１時間で２５題くらいは余裕です。

全部の問題ができるようになるまで終われまテン。

　

step3　確認

目安：１周

参考書の完成具合を見ます。

ここで１周して正答率が９５％をきったらアウト。本当なら全問正解が望ましいです。

　

参考書を完璧にするための最後の一手です。

　

まとめ

今回紹介した方法は

解法暗記

というものです。ネットでは賛否両論ありますが、私は圧倒的に賛成派。

ぜひとも解法暗記で成績を覚醒させてください。