
高校受験、大学受験の場合の数、確率で嫌になるほど出てくる組み合わせの公式nCr。理解できない人にとっては
何回出てくるんだ!
ってかんじですよね。順列と区別もつかないし、「組み合わせだ!」と思ったときはだいたい順列っていう。。。。
ということで、今回は組み合わせの公式nCrの計算方法、使い方、証明について書いていこうと思います。
数学 nCrの意味と公式

nCrの意味は
『n個の中から、順番は考えないでr個取り出す』
例えば、
「A、B、C、D」の4個の中から2個取り出す
ことを考えましょう。
このとき、「AB」=「BA」です。順番は関係ない組み合わせだからです。
そして、これは全部で「AB、AC、AD、BC、BD、CD」の6通りあります。
n=4レベルなら1つ1つ数え上げても解けますが、100個の中から2個を取り出すとかになってくると数えてられません。
そんなときに使うのがnCrです。
分母には全部でr個の
r×(r-1)×・・・1 を書きます。
分子にもr個
n×(n-1)×・・・ と書きます。
4個の中から2個を選ぶときは、
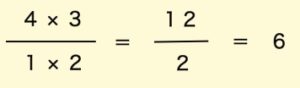
(https://blog.apar.jp/data-analysis/3927/より)
分母には2×1、分子には4×3です。分子は大きい方からr個書きます。
そしてnCrの公式は
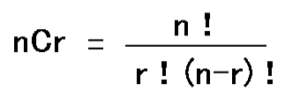
です。
?
こういうことです。
n!=n×(n-1)×…×(n-r+1)×(n-r)×…×1
r!(n-r)!=r×(r-1)×…×1 ×(n-r)×…×1
分母にr個の掛け算、分子にもr個のn×(n-1)×…が必要です。
ただ、分子にn!を置いてしまうと多すぎるのでr個に調節するために分母に(n-r)!を置いたわけです。
実際に計算するときは公式の方ではなく、
分母にr!、分子にr個のn×(n-1)×…にしましょう。
ちなみに、nC₀=1です。
n個の中から0個を選ぶ選び方は、何も選ばないという1通りだけです。
数学 nCrの計算練習

いきなり、問題です。
5枚のカード「1,2,3,4,5」の中から2枚のカードを選ぶ方法は何通りですか。
選んだ2枚の中に順番は関係あるでしょうか。
カードは「1,2」と「2,1」は異なって数えるのか。
今回は「1,2」=「2,1」です。
カードの組み合わせ=セットの数を聞かれているので、順番は関係ないです。ということは、nCrが使えます。
₅C₂=5×4/2×1=10
です。
まとめ
nCr自体難しくはないと思います。
是非、計算練習をいっぱいして順列と組み合わせの使い分けに慣れていってください。










基礎問題精講を4周して一度センター試験の過去問(2019)を解いてみたところ、5割くらいとれました。自分が基礎問題精講を4周した感触としては、例題、演習ともに解放が頭に殆ど入っている感覚だったので8割くらいとれるかな、と勝手に思っていました(今となればチェバの定理、メネラウスの定理など抜け目はありました)。自分としては、失点した部分が確率や図形の部分で、問題によりますが思考力が必要になる問題で、基礎問題精講をこのまま周回していくだけで点は上がるのかと少し不安になりました。慣れで点が上がることもあるので、過去問をもっと解いていこうと思うのですが、5割から慣れで点はどのくらい上がるのでしょうか?拙い文章で申し訳ありません。
まず4周の段階で過去問に入るのはまだ早いと思います。4周で5割なら、おそらく解法の選択速度だったり、処理速度が十分でないゆえの失点が多いと思います。そのまま形式に慣れても10点UPが限度かなと思います。