高校数学ⅠAの単元一覧。単元の特徴！勉強の注意点など！

高校数学にはⅠAがありますよね。その中にも多くの単元、分野に分かれています。

https://high-child.com/2018/11/02/高校数学Ⅱbの単元一覧%E3%80%82単元の特徴！勉強の注意/

そして、単元、分野どうしは関連していたり、独立していたり、勉強しにくかったり、勉強しやすかったりなどなど。

色々な特徴があります。

ということは、今勉強しておかないとヤバイ単元、あとからやれば良い単元があります。

みなさんも、大事な単元、雑魚い単元、みんなの苦手単元などは知りたいと思います。というか、みなさんが知りたいと思っていると信じたいです(笑)。

だから、今回は高校数学の単元の特徴を紹介していこうと思います。

ちなみに、私は独学をしていて、三角比の単元で一度挫折しました。（早いですね笑）

そんな人の役に少しでもたてば嬉しいです。

　

　

高校数学ⅠAの単元、特徴一覧

高校数学ⅠAは

• 数と式
• 集合と論理
• 2次関数
• 図形と計量＝三角比
• 図形の性質
• 場合の数と確率
• 整数の性質
• データの分析

で構成されています。順番に紹介していきます。

　

数と式

難易度：★☆☆☆☆

大事さ：★★★★☆

内容：実数 、 式の展開と因数分解 、一次不等式

＜評価＞

高校数学ではもっとも簡単ですが、「絶対値」、「因数分解」でやられる人が多いです。

例えるなら、マリオのジャンプの仕方が分からずにクリボーにやられる感じです(笑)。

絶対値、平方根では外すときに頭がこんがらがる人が発生。

因数分解も新しい公式、たすき掛けが出てくるんですが、いつ、どう使っていいのか分からなくなる人が多発します。

＜ポイント＞

中学レベルの因数分解は暗算で出来るようになっておくことをお勧めします。

数と式は公式を覚えて使う訓練をすれば、余裕だと思います。ここの内容は高校数学でずっと使うのでしっかりと。

集合と論理

P⇒Q

難易度：★★☆☆☆

大事さ：★★★☆☆

内容：集合、命題、必要十分条件

＜評価＞

集合なら「かつ」と「または」、命題なら「逆」、「裏」、「対偶」と「ある」、「すべて」がわかっていれば余裕だと思うのですが。。。

基本的に日本語と整理力が問われます。

集合は確率や場合の数でも使うのでマスターしておいてほしいです。

必要十分条件は最難関レベルまで来るともう一度気にすることになります。しかし、それまではセンターで出るだけなので、そんなに頑張らなくてもいいと思います。

　

　

２次関数

難易度：★★★☆☆

大事さ：★★★★★

内容：２次関数のグラフ、最大最小、移動、解の配置、２次関数と直線

２次不等式、２次方程式

＜評価＞

高校数学で初めての鬼門です。クッパジュニアくらいです。ワンピースならCP9くらいですかね。

中学校とは各が違うことを見せつけられるでしょう(笑)。２次関数のせいで高校数学が嫌いになる人も多いです。

しかし、２次関数は数学ⅡBでメチャクチャ使いますし、センターでもガッツリ出るので出来ないと先は厳しいと思います。

まあ頑張ってください。

＜ポイント＞

２次関数は

• ax² +bx+c
• a(x+p)² +q
• a(x-α)(x-β)

のどれかで置けば解けることをマスターしていれば、半分は攻略できると思います。

そして、最大最小は

• 頂点
• 軸からの距離

で決まることを知っていれば、この単元の９割は出来ると思います。

　

　

図形と計量＝三角比

（一応、画像は三角形ですね(笑)）

難易度：★★★☆☆

大事さ：★★★★☆

内容：三角比の値、三角方程式、三角不等式、正弦定理、余弦定理、三角形への応用

＜評価＞

完全に新しい概念なので、独学だとつらいです。三角比は辺と辺の比であることを忘れなければ中々行けると思います。

三角比もセンターでバリバリ出るし、ⅡBの三角関数はもろ三角比の上位互換なので、ここで躓くとちょっとヤバイ。

あと、公式は使っていく中で暗記したり、意味を考えていかないと追いつかなくなります。

＜ポイント＞

三角比は辺と辺の比であるということをおさえないと、理解に苦しみます。それでも苦しむかもしれない。

あと、公式は丸暗記しようとしても、量が多いし複雑なので覚え間違えます。使いながら覚えましょう。

三角形の面積公式などはsinθの意味を考えれば覚える必要はないです。そうやって少しずつ覚える量を減らすのがコツです。

　

　

図形の性質

難易度：★★★☆☆

大事さ：★☆☆☆☆

内容：５心、接弦・方べきの定理、チェバ・メネラウスの定理、内・外接球、円、立体

＜評価＞

中身はほぼ全部「平面幾何」＝図形の問題です。

この分野がほかの分野と融合したり、応用されたりすることは少ないです。出来なくても問題ないですが、これは数学的センスも大事なので出来れば勉強しておいてほしい。

ほとんどでなく、出ても難問なことが多いので受験にはあんまり関係ないです。

独学する人は時間がなければ飛ばしてもいいくらいです。

＜ポイント＞

中学校で習った平面図形の性質を思い出しましょう。

重心、内心、外心、垂心、傍心の５心は性質が多いので、勉強するならしっかりと抑えておきましょう。

問題をたくさん解いて慣れるのが最短経路だと思います。

　

　

場合の数と確率

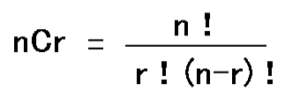
難易度：★★★★★

大事さ：★★★☆☆

内容：順列、組み合わせ、重複組み合わせ、道数え、確率

＜評価＞

場合の数は簡単ですが、確率は問題によって難易度にかなり差があります。確率は東大でも頻出なレベルです。

数学力のある、ないが一番出ます。

ただ、入試に出ない学校は出ません。だから志望校に確率が出るかでないかは確認しておいた方が良いと思います。

しかし、センターではバリバリ出ます。大問一個分です。

＜ポイント＞

出てきた考え方、公式の意味をしっかり考えましょう。分からなければ、友達か先生にしっかり質問しましょう。

一番最初の関門はP（順列）とC（組み合わせ）の使い分けです。意味が分かっていれば簡単ですが、わかってないと全然意味不明だと思います。

中ボスに「確率の最大値」です。これは意味を考えるのが少々難しいかもしれません。是非、だれかに質問しましょう。

ラスボスは「条件付確率」です。丸暗記だと後々本当にわけわからなくなります。

センターレベルなら丸暗記でも解けますが。。。

　

　

整数の性質

難易度：★★★★★

大事さ：★★☆☆☆

内容：約数や倍数、ユークリッドの互除法、不定方程式、mod、n進法、ガウス記号

＜評価＞

使っている式や公式は単純なんですが、思考の部分が難しいです。

こちらも、問題によって難易度にかなり差があります。

難関大学で出る整数は激ムズですが、センターレベルなら典型問題を網羅しているだけで解けると思います。

＜ポイント＞

不定方程式やn進法は個別でしっかり演習を積むことをお勧めします。

あと、倍数判定法は覚えておきましょう。余裕がある人は証明までした方がいいと思います。

２の倍数：下1桁が２の倍数

３の倍数：各桁の和が３の倍数（123なら1+2+3＝６）

４の倍数：下2桁が４の倍数

５の倍数：下2桁が５の倍数

６の倍数：２の倍数かつ３の倍数

・・・・・・などなど。

　

　

データの分析

難易度：★☆☆☆☆

大事さ：★★☆☆☆

内容：ヒストグラム、四分位数、分散、標準偏差、相関関係、散布図

＜評価＞

データの分析はセンターでしか出ません。

勉強しておいて損はないですが、受験前になって急いで詰め込んでも間に合います。

＜ポイント＞

ある程度は問題を解いて、練習しておきましょう。

相関係数などは計算量が多いので、計算ミスをしないようにしておきましょう。

あまり時間をかけて勉強する必要はなく、こちらを一生懸命やるなら２次関数をやってほしいくらいです。

　

　

まとめ

是非、私の独断と偏見によるアドバイスを役に立てて勉強してください。

今日の名言

才能で負けるのはまだ言い訳が立つ、しかし誠実さや、勉強、熱心、精神力で負けるのは人間として恥のように思う。他では負けても、せめて誠実さと、精神力では負けたくないと思う。

武者小路実篤

　

↓の記事は２Bの記事になります。よければぜひ。

https://high-child.com/2018/11/02/高校数学Ⅱbの単元一覧%E3%80%82単元の特徴！勉強の注意/