平方根とは何ぞや。
中学数学になっていきなり出てくる謎記号
「√」
こいつのせいで数式が謎の方向に進んでいく。
先生が「ルート」という度に、話が分かりにくくなっていく。
そもそも何が起こってるのか、何をしたらいいのか分からない。
算数はできたのに急に抽象的になって、イメージしにくくなった。だから数学が苦手になりかけてる。
そんな人に今回は「平方根」を分かりやすく解説しようと思います。
もちろん、算数もできなかった「数弱」の方にもわかるように解説しますw
最初は平方根から説明するので、分かる人は適当に飛ばしてください。
目次
平方根とは?
いきなりですが、質問です。
□×□=4
※□には同じ数字が入ります。
□には何が入るでしょう?
なめてんのか、って思う人もいるかもしれませんね。「□=+2」です。
そして、負の数を習った中学生なら「□=-2」でも成り立つがわかるはず。試しに□にいれて計算してみてください。
(-2)×(-2)=2×2=4
つまり答えは□=±2
じゃあ、
○×〇=25
はなんでしょう?
〇=5ですね。もちろん、〇=-5でも成り立ちます。
では、聞き方を変えます。
4の平方根は?
翻訳すると、「2乗して4になる数は?」つまり「4=□×□ の□は?」ということです。
つまり答えは
±2
じゃあ、
25の平方根は何でしょう?
±5ですね。
平方根の意味はもう分かりましたよね。
「2乗するとAになる数」をAの平方根
っていうんです。
4の平方根は±2
9の平方根は±3
16の平方根は±4
でもこれは特別な場合。
7の平方根は何でしょう?
ここで謎記号「√」が登場します。
答えは、±√7
2乗してAになる数=±√A
という約束で「√」を使うんです。
ルートの計算
ということは、
25の平方根は
±√25なのか?
答えはYes。
さっきの答えは±5でしたよね。
「√25=2乗すると25になる数」
25=5×5
つまり2乗すると25になる5は、√25の答えなんです。
√25=5
ルート計算と平方根の違い
ここでまさかの事態発生。
「4の平方根=±2」ですが、「√4=2」なんです!
実はルート(√)は「正の平方根」を表すんです。
平方根って2つありますけど、数字の部分は一緒じゃないですか。「+」か「-」かの差だけですよね。
「+」の方は0より大きいから正の数。だから正の平方根って呼ぶんです。
- 平方根は「+」と「-」の両方
- √は「+」だけ
だから
√9=3
√16=4
√25=5
あと、「√Aは2乗するとAになる数」ですよね。正の平方根だから。
つまり、
√A×√A=A
が成り立つんです。
17=√17×√17 とも表せます。
ルートの求め方
たった1つのお約束
- √は掛け算ならバラバラに分解できる
つまり、
12=2×2×3なので
「√12=√2×√2×√3」に分解できる
そして√Aは2乗するとAになる数。
√A×√A=Aですよね。だから、√2×√2=2
√12=√2×√2×√3
=2×√3
計算練習
√18を簡単にしなさい
18=2×3×3
√18=√2×√3×√3
=√2×3
つまり
√18=3√2
√24を簡単にしなさい
24=2×2×2×3
√24=√2×√2×√2×√3
=2×√2×√3
=2×√6
ここで注意点。
√6=√2×√3に分解できるので、もちろんその逆に「√2×√3=√6」もできます。
で、答えは
√24=2√6
ルートの計算 足し算・引き算
足し算・引き算のお約束
足し算、引き算でのお約束も1つ。
- 同じ√でしか足し引きできない
√2+3√2=(1+3)×√2
=4√2
これは、
「X+3X=4X」みたいなもんです。
でも
√2+3√3=√2+3√3
で全く式を変えることが出来ません。
√2と√3どうしでは足し算引き算はできないんです。
粘土と粘土板みたいなもん。粘土と粘土版をくっつけたって、その”合成されたもの”は粘土にも粘土板にもならないじゃないですか。
くっつけたって粘土と粘土板でしょ。
√2が粘土で、√3が粘土板なんですよ。
はい。
わけわからん例え話に付き合ってもらってありがとうございましたw
計算練習
2√3+5√3-3√3 を計算しなさい。
これは非常に簡単。
(2+5-3)×√3=4√3
簡単ですね~
7√5+3√2+4√5-4√2 を計算しなさい。
まずは√5から片付けていきます。
7√5+3√2+4√5-4√2
=(7+4)×√5+3√2-4√2
=11√5+(3-4)×√2
=11√5-√2
最後は、粘土と粘土板なのでこのままでOK。
√18+√50+√8 を計算しなさい。
パッと見既につんでるんですよ。
でも、よ~く考えてください。√18も√50も√8もより分かりやすい形にできます。
√18=√2×√3×√3
=3√2
√50=√2×√5×√5
=5√2
√8=√2×√2×√2
=2√2
まさかの√2ぞろい
ってことで。
√18+√50+√8 =3√2+5√2+2√2
=10√2
ルートの足し算・引き算の手順は
- 簡単な形に√を整理
- 同じ√で足し算、引き算
ルートの計算 掛け算・割り算
掛け算・割り算のお約束
- √A×√A=Aになる
- 分母に√が来たら、有理化する
まあ、掛け算の方は
√6=√2×√3だから、逆の√2×√3=√6も成り立つよ。つまり、√を無視して掛け算しても大丈夫だよ。
とお話ししました。
次は
新しい用語「有理化」です。
あ~また来たよ。
とか思わないでください。
平方根・ルートの中ではこれが最後です。
有理化っていうのは、分母に√が来てしまったときに分母の√を消す作業です。パソコンで分数打つと変になるので、写真でいきます。
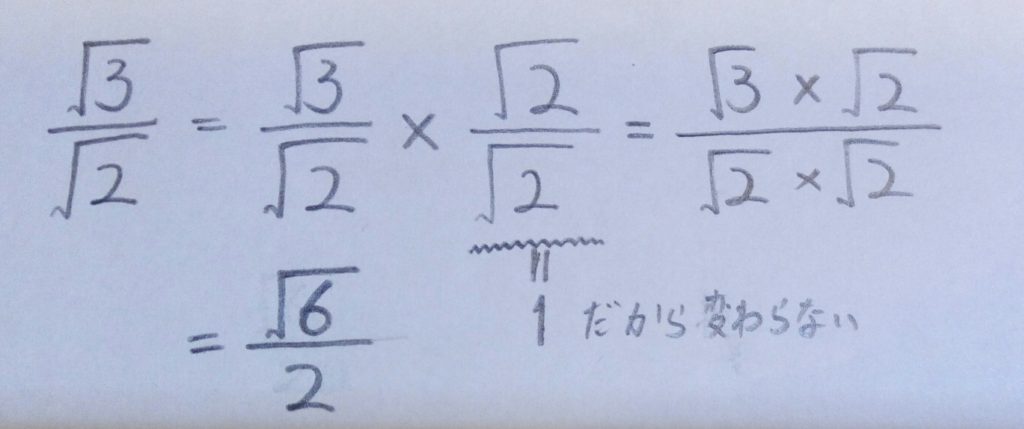
こういう作業を有理化っていうんです。
なんでか数学の世界では分母に√が来るとなくしたがるクセがあるんですよね。
まあ作法みたいなもんです。
計算練習
√6×√15×√12 を計算しなさい。
めちゃめちゃ計算頑張って、
√6×√15×√12=√1080
=6√30
ってやった人手上げてください。
それは大変すぎ。
ポイントは
- 簡単な形に√を整理
- √A×√A=Aで計算する
√6×√15×√12
=(√2×√3)×(√3×√5)×2√3
=3×√2×√5×2√3
=6×√2×√5×√3
=6×√30
=6√30
√8×√14×√10÷√21 を計算しなさい。
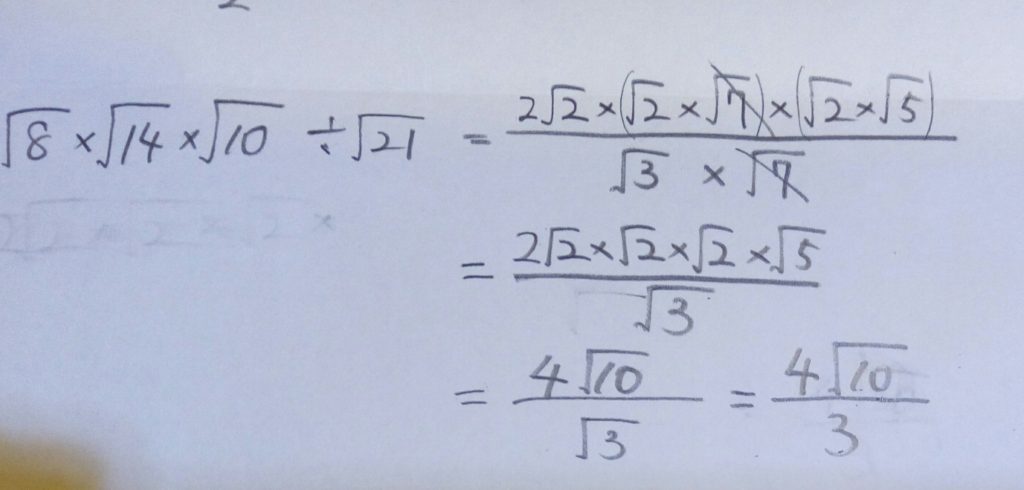
たいして難しくないので、大丈夫だったと思います。
まとめ
平方根、ルートは理解できましたか?
一度掴んでしまえば、そんなに難しくないです。
あとは練習あるのみ。
ひたすら繰り返してれば、勝手に脳が計算できるようになるので頑張ってください。










はじめまして。ルートの説明とてもわかりやすくて、はじめて理解できました!ありがとうございます。
最後の問題の答えが 多分 4√30÷3 だと思います。
わかりやすい解説 本当にありがとうございました。
間違いが指摘できるくらい理解しておられるとは素晴らしい!(精一杯の強がり、普通にミス気付かなかった)ご指摘ありがとうございます。