数学になると、謎の数字の分類がありますよね。
素数、自然数、整数、有理数、無理数、…
いや、いきなり出てきといて謎すぎ!
もうちょっと真面目に説明してから使ってくれよ。なんで急に謎い分類で問題を解かせようとするんだよ。
わけわからんて。
そんな人も多いかと思うので、今回は数字の分類について説明していきたいと思います。
目次
数字の分類
数字には
- 素数
- 自然数
- 整数
- 有理数、無理数
- 実数
- 複素数
があります。
上から順に集合が大きくなっていきます。
簡単に言ってしまえば、素数が一番少なくて、複素数が一番多いということです。(正確には違いますが)
↓みたいな感じになってます。
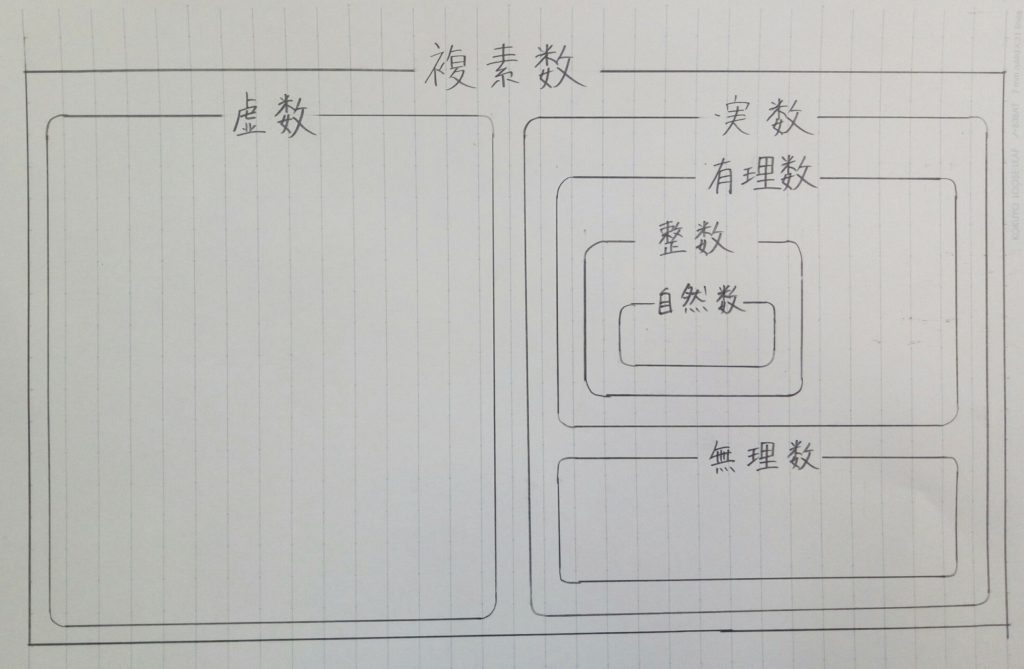
複素数=学校
虚数=特別支援学級、実数=普通学級
有理数=1年生、整数=1組、自然数=イツメン
無理数=2年生
みたいな感じです。
素数とは
例)2、3、5、7、11、13、17、19、…
記号:P
素数とは
1と自分自身しか約数を持たない数
のことです。
はい、わけがわかりませんねw
例えば、13について考えてみましょう。
13は当然ながら、1で割り切れます。そして自分自身である13でも割り切ることが出来ます。
7も1と7でだけ割り切れます。
1と自分自身で割り切れるのはごく当たり前で、それ以外に割り切れる数がないものを素数と言います。
言い換えれば
約数が2つしかない数。
小学生のころに、長方形の面積を□でわけて掛け算で表すやつをやりましたよね。
2×3=6なら、こんなふうに
でも、素数だと1×5=5のように
ただの横一列のクソつまらない長方形しか作ることが出来ません。
長方形にしたときに横一列のものしか作れない数は素数です。
ちなみに、1は素数ではないです。
「1と自分自身しか約数を持たない」or「2つしか約数を持たない」数が素数でしたよね。
約数を1しか持たないと素数にはなれません。
自然数とは
例)1,2,3,4,5,6,7,8,9,10…
記号:N
自然数とは
正の整数のこと
1に順に+1をしていってできる数の集合を自然数といいます。
基本的には、
無人島生活をしていて使いそうな数は全部自然数です。
あ、リスが1匹いた!
木が2本倒れている。
ヤシの実が3個ある!
みたいな。
そして、0は自然数には入りません。
コウモリが0匹いる!
みたいな発言はしないですよね。
0を無人島生活で使うなら「なんもない」と言うから、0という数字は使わないと思います。
整数とは
例)…-2、-1、0、1、2…
記号:Z
0から順に±1をしていって出来る数を整数と呼びます。
「マイナスの自然数」と「0」と「自然数」=「整数」
キレイな数は全部整数。
なんか好きな数言ってみてと言われたときに言う数字は、整数です。いわゆる普通の数です。
まあそれでもマイナスの数を言う人はいないと思いますけどねw
ちなみにですが、自然数はすべて整数ということになります。
有理数・無理数とは
有理数とは
Q/P
Qは整数、Pは自然数で表される数です。
簡単に言えば、分数です。
5のような整数だって、5/1のような分母が1の分数ですよね。1.5=3/2のように分数で表せるので、有理数ということになります。
有限小数は分数で表せますもんね。
他には、0.123123123123…のように循環する小数も分数であらわすことができるんです。
高校生になれば数学で習います。
分数で表せる、整数・有限小数・循環小数は有理数ということになります。
では、問題。
「-26.71」「0」「12.08080808…」「√5」
の中で有理数はどれでしょう。
分数で表せるもの。つまり、整数・有限小数・循環小数を探して行けという問題です。
答え:√5以外の3つ
「-26.71」有限小数ですよね。だから有理数です。
実際、分母を100にすれば、-2671/100という分数になります。
「0」は整数なので有理数。
分母は何でもいいですが、分子を0にすれば、0/a=0で分数で表せますよね。
「12.08080808…」は小数点以下で「08」が繰り返す循環小数なので、有理数です。
X=12.08080808…とおけば、
100X=1208.08080808…
- X= 12.08080808…
99X=1196
ということで、X=12.08080808…=1196/99 と分数の形で表すことができます。
最後に
「√5」は
√5=2.236067977…
と不規則に無限に続く小数です。そのため、有限小数でもないし、循環小数でもないです。
もちろん整数でもないです。つまり有理数ではない。
無理数
ということになります。
無理数というのは
π=3.14159265…
e=2.71828182
や√の数です。
πは知っての通り円周率。eは微分しても変わらないという意味不明な数。ネイピア数ともいわれます。
高校生の問題で無理数と言われたらほぼほぼルートの話なので、意味不明な数は気にしなくていいです。
ちなみに無理数の定義は
実数のうち有理数でないもの
分数で表せない数は無理数です。
実数とは
実数は
有理数と無理数を合わせた数です。有理数の中には当然、整数や自然数なども入っています。
今まで紹介してきた数すべてが実数に含まれます。
虚数とは
虚数は
iが入っている数字のこと
です。
X2=-1となる数を虚数「i」とおいて、作り出した幻の数です。
そのため現実世界で「i」を見つけることはできません。想像上の世界での数字です。
そんな数字たちを虚数と呼びます。
「i」を含む数字どうしには大小関係もなく、非常に意味不明な数です。
数学ⅡBで習います。
複素数とは
すべての数の親玉みたいな感じ。
どんな数も複素数です。
p+qiで表せる数
pもqも実数です。
実数はq=0のときです。
すべての数は複素数の派生。鬼滅の刃の鬼舞辻無残みたなやつ。
まとめ
これが数字の分類です。
世の中の数は上のように分類されています。
これであなたも数字分類マスター。
進研ゼミ風に何でもマスターつけとけばいいと思っている奴。