2020.4.3
なんと、
未解決問題「ABC予想」の一部が証明されました。
パチパチパチパチ。
正直言って、どうでもいいですねw。
はい。
でも、
それじゃあ望月新一さんも可哀想なので、今回はできる範囲まで「ABC予想」を解説しようと思います。
「ABC予想」を理解するだけなら、そこまで難しくないので安心してください。
目次
「ABC予想」の証明者
望月新一とは?
よくわからんけど、
「望月新一すげぇ」
では可哀想。
まあ本当の凄さは本人レベルの頭脳でないと分からないでしょうが、ある程度は理解を深めたい。
ということで、
望月新一さんの今までを振り返ろう!
望月新一の経歴
0歳 日本に生まれる
5歳 父親の仕事でアメリカへ
13歳 エクセターアカデミー
に2年在学
16歳 プリンストン大学に飛び級入学
19歳 同大学の学士課程を卒業(次席)
23歳 同大学の博士課程を修了
日本へ帰国
京都大学の助手に採用
27歳 京都大学の助教授に昇格
32歳 京都大学の教授に昇格
43歳 宇宙際タイヒミューラー理論
をHPに上げ発表
51歳 「ABC予想」を証明
望月新一の驚きポイント①
まず「驚きポイント①」は、
中卒でプリンストン大学へ合格
途中で2年間在学した「フィリップス・エクセター・アカデミー」というのは、中学校です。
しかも中学校に2年間しか通わない。
そのまま世界的トップ大学のプリンストン大学に飛び級で合格。
プリンストン大学ってアメリカ大学ランキング1位を何度も取っている最強の大学です。
卒業生には
- ケネディ大統領
- GoogleのCEO
- AmazonのCEO
などがいます。
望月新一の驚きポイント②
そして「驚きポイント②」
「プリンストン大学を次席で卒業」
要するに、
プリンストン大学を2位の成績で卒業したってこと。アメリカの大学は全員ガチで勉強するので、入学してからが大変です。
そんな奴らを倒して、2位。
飛び級で入ったことも忘れずに。
望月新一の驚きポイント③
そんでもって「驚きポイント③」
「32歳で教授に昇格」
親戚に教授でもいないと分かりにくいですが、
30代で大学教授になるというのは超レアケースです。
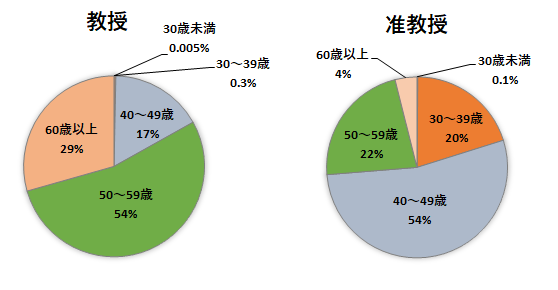
上の左の円グラフを見れば分かりますよね。
30~39歳の教授は0.3%です。一時期、31歳で教授になった人がその時最年少で話題になりました。
その後、26歳で教授になった人もいましたが、超絶例外。
基本は30歳前後で教授になれば、最年少クラスです。
望月新一の驚きポイント④
一番すごいのが、
「宇宙際タイヒミューラー理論を発表」
です。
「宇宙際タイヒミューラー理論」というのは、望月新一さんが自分で作った理論です。
凄いのが、
発表した当時では、理解できる人が世界に数人しかいないと言われていたことです。
「宇宙際タイヒミューラー理論」が発表されたのはいいですが、みんな正誤を判定できないという状態。
最近になって、
やっと理解されて本になりました。
私は読んだことがないですが、一般人でも一応理解できるように書かれているらしいです。
でも、多分99%私にはムリですw
「ABC予想」とは?
「ABC予想」の概要
まあ「ABC予想」っていうのは、
「最も重要な未解決問題の1つ」
というわけです。
「ABC予想」というのは、
1985年に数学者ジョゼフ・オステルレとデイヴィッド・マッサーの2人のよって提起された予想です。
予想なので、
「多分こうなるんじゃね?」みたいに、気楽に言い始めたわけです。
でも
「ABC予想」を使うと、数多くの有名な理論や予想を即効で導き出せるのです。
だから、
どうしても「ABC予想」を証明したい。
ということで、
「最も重要な未解決問題の1つ」と呼ばれるようになったわけです。
そして、
2020年4月3日まで解き明かされなかった。
「ABC予想」の内容
「ABC予想」というのは、
a,b,cは互いに素な整数であり、
a+b=cを満たすとする。このとき、
max{|a|,|b|,|c|}<(rad(abc))2
が成立する。
という内容です。
意味わからないと思うので、1行ずつ日本語訳していきます。
「a,b,cは互いに素な整数であり、」というのは簡単ですよね。「a,b,cには共通する約数がない」ということです。
「4,8,18」なら約数2を持っていますよね。だからダメです。
「3,5,7」なら共通な約数を持っていませんから、「3,5,7は互いに素」というわけです。
そんでもって、
「a+b=cを満たすとする。」らしいです。
そして、
「max{|a|,|b|,|c|}」というのが謎記号ですね。
「|a|」というのは「aの数字の部分」です。「|5|=5」だし、「|-4|=4」です。数字の部分だけ拾ってきます。
だから
「max{2,-3,4}」なら「max{2,3,4}」ということです。
「max{a,b,c}」というのは「a,b,cのうち最大の値」というわけ。「max{2,3,4}=4」ですね。
最後に、「rad(abc)」について。
「rad(X)」というのは「Xの素因子積」という意味。
素因子というのは、
例えば「12」なら、「12=22×3」なので素因子は「2と3」です。「84」なら「84=22×3×7」なので「2と3と7」です。
「rad(12)=2×3=6」「rad(84)=2×3×7=42」というわけです。
ですが今回は、
「(rad(abc))2」なので、出てきた値を2乗します。
まとめると
a,b,cには共通する約数がなく、
a+b=cを満たす整数であるとき、|a|,|b|,|c|のうち最大値が
abcの素因子の積の2乗より大きい。
「1,2,3」で試してみると、
1,2,3には共通約数がなく、
1+2=3max{|1|,|2|,|3|}=max{1,2,3}
=3(rad(6))2=(2×3)2
=62
=363<36
成り立っている。
内容は大して難しくないですよね。
操作は中学数学レベルです。
でも、
証明は絶対ムズイのは分かります。初手が1つも思いつかないですからねw
実は望月新一は証明してない
最後に話の骨を折るようで申し訳ないですが、
望月新一は「上のABC予想」を証明してない
実は、
望月新一が証明したのは、
『任意のε>0に対して、ある正の定数K(ε)≧1が存在して、次を満たす:
「本がすき。」より
a,b,cを互いに素な整数でa+b=cを満たすならば、不等式、
max{|a|,|b|,|c|}< K(ε) (rad(abc))^(1+ε)
が成立する』
という
「ABC予想」の派生版です。
なんなら、
派生版の方が難しいです。私も言っている意味が分かっただけで、表面しかわかってません。
だから
説明できません。
すいません。
ということです。
まとめ
え、終わり??
て感じですが、私はすべて出し切りましたw
あとは自力で理解してください。
では、
力不足ですいませんでした。









