今回は、数学の薄い問題集・参考書について紹介していこうと思います。
なぜ、青〇ャートみたいな信頼とページ数が厚い問題集を使わないのか。
それは、
中途半端になるからです。
結局、受験数学は「完璧にした問題集の数」＝「数学力」の世界です。
青〇ャートを中途半端にやるなら、薄い問題集を何周も何周もして完璧にした方が１００倍成績は上がります。
上記のことに気づいた私は、数学の参考書・問題集をあさりまくり、最強の薄い問題集を見つけてしまったのです。
それが基礎問題精講。
目次
数学の問題集なら基礎問題精講
いきなり体験談から始まりますが、興味ない人は飛ばしても記事の内容に差はないですｗ
網羅系の鬼「青チャート」
私はある日、数学で無双しようと考えました。
そのために勉強法をネットであさっていたところ、ある情報が多く出ていることに気づきました。
「青チャート→１対１→プラチカ」で東大にも合格できる。
という情報です。
私はその情報を信じて、さっそくヤフオクで青チャートを約５０円＋送料500円で買いました。
そして、やる気満々で青チャートを進めていったのでした。
来る日も来る日も毎日５例題ずつ青チャートを進めていく日々。部活があっても、試合があってもひたすら進む。
毎日、新たな解法を求めて進む。
例題を考えて、解説を読み、頭にストックしていく。
１ヶ月後。
私の精魂は尽き果てていました。
世界は灰色。
青チャートの解説はただのきごうの羅列。
そんなに疲れて１か月間勉強したのに、なんと言うことでしょう。
まだ例題１３５！？
私のすべてをかけても、まだ半分もいっていない！？
青チャートは全部で３周する予定だというのに、１周目の前半で燃え尽きてしまっている。
こうして、青チャートを章ごとに引き裂き、捨てました。
↑に共感した人は、ぜひともこの記事を最後まで読んでください。必ず役に立つ内容にしています。
なぜなら、私の体験談が元だからｗ
数学 基礎問題精講の対象者
ずばり、
- 高３で時間がない
- 厚い参考書・問題集はうんざり
- 基礎固めをしたい
ような人におすすめです。
こんなの数学が苦手な人は全員当てはまりますよね。得意な人でも、手軽に基礎固めが終わるのでおすすめです。
特に数学Ⅲを勉強する人は、薄い問題集の方が高速周回ができて効率的。
数学 基礎問題精講の問題数
| 参考書 | 例題 | 練習問題 | 章末問題 | 合計 |
| 基礎問題精講 | 145 | 145 | － | 290 |
| 青チャート | 329 | 329 | 293 | 951 |
※わかりやすいよう、青チャートと比較
※どちらも1・Aのもの
これからわかるように、青チャートって1000題もあるんですよ。
1000題もやったら、基礎問題精講３周もできますよ！
確かに青チャートは網羅性は素晴らしいです。でも、量が多くて終わりません。やり切れず、挫折してしまっては意味ないですよね。
数字で見ると、基礎問題精講の薄い具合がよくわかる。
そして網羅性は欠けていません。
基礎問題精講はその名の通り、基礎にある重要問題を厳選して、しっかり全範囲を網羅できるようにしています。
それぞれの問題は重複することなく、全体を網羅。
青チャートは
- レベルの幅が広すぎる
- 重複する問題が多い
から問題数が多いだけ。
青チャートは薄く広くやりますが、基礎問題精講は本当に重要な部分だけを深く掘り下げます。青チャートが板書で、基礎問題精講がまとめノートみたいな感じです。
数学 基礎問題精講のレベル
レベル：教科書～MARCH弱
到達レベル：共通テスト８～９割
わかりやすく言い直します。
共テ８割～：使う必要なし
共テ７割〜：微妙だが、使った方が良い
共テ４割～：迷わず使うべし
共テ３割〜：理解力に自信があればどうぞ
それ以下：「とってもやさしい数学」から
基礎問題精講が網羅しているレベルは、まさに共通テスト（センター試験）レベル。
ドンピシャです。
共通テスト（センター試験）対策、数学の基礎をマスターするには丁度良すぎるレベルに位置します。
そして数学は基礎を抜けなく完璧に網羅してしまえば、応用問題もドンドン解けるようになります。
数学の基盤になるのが「基礎問題精講」。
数学 基礎問題精講の特徴
基礎問題精講は
「例題」＋「精講」＋「解答」＋「ポイント」＋「演習題」で構成されています。
そして、「精講」と「ポイント」は基礎問題精講の中でも特徴的なので、紹介しようと思います。
①精講がハイクオリティ
実は、基礎問題精講の一番の特徴で、もっとも役に立つのがこの「精構」です。
「精講」には、例題を解く上での「注意点」「方針」が約3～１５行で書かれています。
・絶対値の問題なら、絶対値の外し方。「ax=b」のような問題なら、本当にaで割って良いのか。
・順列なら、どのような手順・考え方で文字の場所を決めていくか、並べていくか。
その問題を通して「注意して学ぶべき核心」が書かれていると言ってもいいでしょう。
この「精講」は問題を解くときの視点や考え方が書いてあります。
だから
解法の丸暗記になることなく、数学ができる人の見ている世界も知ることが出来ます。
②ポイントが超便利
「解答」のあとに「ポイント」という、
- 使った公式
- 解答の流れのまとめ
などが書いてあります。
問題がまだ上手く解けないときは、このポイントが大変便利です。「あれ？加法定理なんだっけ？」というときに役に立ちます。
しっかり覚えてもいない公式で悩んで、時間を使うなら、さっさと公式を見て覚えた方が効率的です。
また、解答の要点を１通り把握したいときは、非常に役に立ちます。
数学 基礎問題精講の効果
実際、基礎問題精講でどこまで数学が伸びるのか。
私の場合は、
３ヶ月で偏差値７０までUP
「どうせ最初から数学得意だったんだろ？」
「駿台模試受けた後に進研模試受けたんだろ？」
とか思う人も多いと思います。
しかし、
私は元々、「教科書の例題なら解けるかな？」くらいのレベルで、そのころの数学の最高偏差値は５４でしたｗ
証拠ですが、
偏差値５４のとき
↓
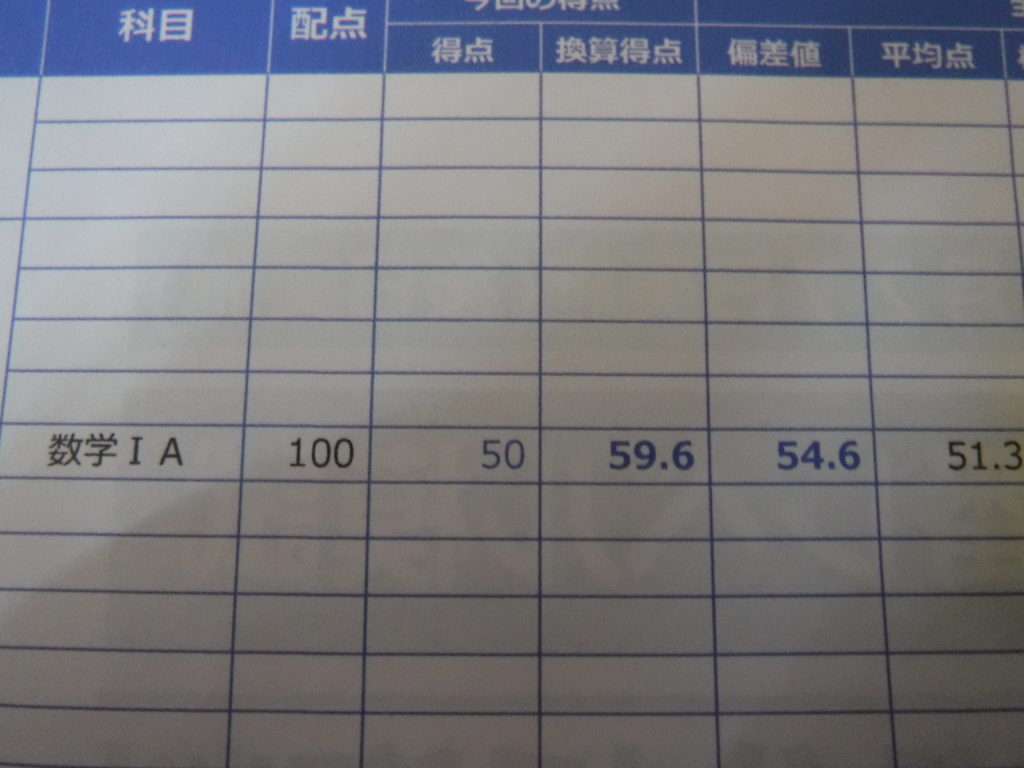
偏差値７０のとき
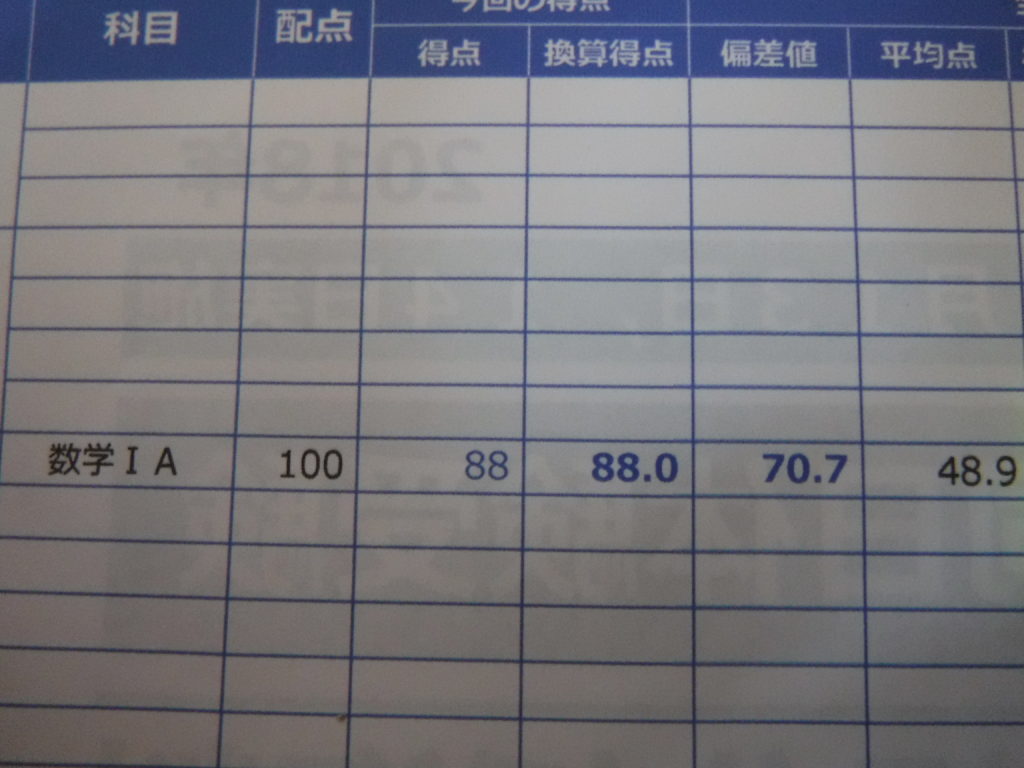
どうして、３ヶ月で偏差値７０まで伸びたのか。
それは、
基礎問題精講にある問題をすべて一瞬で完璧に解けるようにした。
ただただ３ヶ月間、基礎問題精講を毎日解きまくった。
何周もすることになるので、ドンドン解く速度は上がっていき周回速度が上がっていく。
間違えていた問題を復習する頻度も上がっていくので、完成度も上がっていく。
そうして基礎問題精構を本気で極めれば、共通テスト（センター試験）を問題を解く能力はしっかりつきます。
実際は、時間も短いので計算ミスややり残しがあって100点が取れるとは限らないわけですけど。
数学 基礎問題精講の使い方
基礎問題精講には数学ⅠA、数学ⅡB、数学Ⅲと３冊ありますが、１冊ずつ極めていきましょう。
- 例題だけ繰り返す（目安４周 ８０％理解）
- 演習問題だけ繰り返す（目安４周 ８０％理解）
- 例題と演習を交互に（目安２周ずつ ９０％理解）
- 間違い直し
目安期間：３ヶ月/１冊
問題を解いて間違えたら「×」を書いてことおおすすめします。（もちろん解説は理解しながら読んでください）
基本的には「次は出来るようになるでしょ」くらいの気持ちで解けばいいのですが、あんまり間違えてしまう問題はしっかり勉強しないといけません。
その目安として×を書いておくと何回間違えたかわかるね、ということです。
「そんなことよりやる量多くないか」
と思った人いると思います。
でも、普通の人はこのくらいやらないと体にしみこませられないです。体にしみこむまで解かないと次やるときには忘れてしまうし、次のレベルに行けないです。
一番初めにいった通り、
「完璧にした参考書の数」＝「数学力」
です。
そして、同じ問題を解いているので周回数が上がるほど解くスピードが上がります。
２周目は１周目の８０％くらいの時間で終わると思います。そして、３周目も２周目の８０％・・・・・
こんな風に。
私も最後の方は、１時間で２５題解けるようになっていたので、例題だけなら６時間で一周できますね。
６時間でⅠAを一周できるなんて、やっぱり薄い！青チャートでは不可能な次元です。
↑で紹介したやり方は実は私がやったときの使い方です。でも実際は
- 短期間で高速周回
- まず理解
- 最低５周以上
を守って、↓の記事に目を通してくれたら他の使い方でも問題はないです。
紹介した使い方はあくまで１例なので、よくわからない人はマネすると良いかと思います。
数学 基礎問題精講の接続
＜この前にやるべき参考書＞
- 学校の授業レベル
強いて参考書をあげるなら、「ひとつひとつわかりやすく」などです。スタディサプリの授業と併用することも可能だと思います。
＜この次に出来る参考書＞
- １対１対応の演習
- 標準問題精構
- チョイス
私のおすすめは一対一対応の演習です。理由は、一番問題数が少ないからです。一冊も薄いですしね。
他にも薄い問題集ではダメなの？
10日あればいい
他に『10日あればいい』がありますよね。これは基礎問題精講より薄いです。
たぶん、
どこかのサイトで薄い問題集なら１０日あればいいだろ！みたいなものを見たと思います。
単刀直入に、「１０日あればいい」の欠点を申し上げます。
- 薄すぎる
- １冊のカバー範囲が狭い
この２つは共通する部分も多いですが、「１０日あればいい」は薄すぎる。「基礎からexpress」はセンター50％の到達レベル、ノーマルは限度が65％くらい。
数学が苦手な人のために薄く薄くしすぎた結果、網羅性に欠けます。
そもそも私が基礎問題精講をおすすめする理由は「薄い」かつ「網羅度が高い」という一見矛盾したスーパー参考書だからです。
その凄さにはどちらも遠く及びません。
ひとつひとつわかりやすく
確かに薄いです。
しかし、レベルは教科書レベル。センター50％前後が到達レベルです。
となると、「ひとつひとつ」を完璧にした後にもう一度センターレベルの参考書をやることになるので、２度手間です。
多くの人にとっては必要のないレベルが収録されているので、無駄が多いと思います。
※センターで３割前後という人は、「ひとつひとつ」から始めることをおすすめします。
薄い問題集を完璧にすると…
いままで７０点くらいで威張ってきたあの友達。
同じくらいの点数で謎の仲間意識が芽生えかけたあの友達にも、
自分「お前ら何点？」
A君「いやー。言えないよ。お前は何点なの？（心中：俺６２点だけどワンチャン勝ってる説。先に言わせよ）」
自分「おれ９０点。( ･´ｰ･｀)ドヤ」
A君「・・・」
周りの人「え、マジであいつ９０点なの」
自分「お前らの点数、まるでゴミのようだ！！ハハハハハ」
と出来ます(笑)。
なんと言うかは別にして、他の人の見る目が変わるのは確かです。（あんまりドヤると悪い方に見る目が変わっちゃいます(笑)。）
基礎問題精講を３か月やって、数学の基礎を完璧にしておけば楽なもんです。
学校の定期テストはノー勉でも９割超え。模試も数学は自信をもって、高い偏差値をとれる。
今まで数学を勉強していた時間が、
- 英語、国語などの他教科の勉強に
- 趣味に
- youtubeやTwitterなどに
と、自由に使えるようになります。
英語や国語を勉強すれば、当然勉強時間も増えるので、成績は上がると思います。
数学UP → 英語UP →…
と正のスパイラルに入ると思います。そうすれば、受験まで成績は上がりつづけるでしょう。
別に勉強しなくても自由時間として使えば、受験勉強で疲れた体を休ませることができます。
休憩で回復した分、他の時間の勉強効率もどんどん上がると思います。
どちらにせよ、数学を基礎問題精講で完璧にしておくことで、あなたの勉強は一気に楽になるはず。
ぜひぜひ、基礎問題精講を使ってみてください。
まとめ
ということで、分厚い参考書なんてさっさと捨てて基礎問題精講で偏差値70目指して頑張ってください。
今日の名言
目標を達成するには、
全力で取り組む以外に方法はない。
そこに近道はない。
マイケル・ジョーダン
基礎問題精講を毎日進めること意外の方法は存在しません。
単元別に苦手をつぶしたいなら「面白いほどわかる」シリーズがおすすめ。
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 【大学受験 数学】スタディサプリ数学の詳細と使い方を徹底解剖！ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 例題だけはヤメろ！『１対１対応の演習』を吸い尽くす使い方＆レベル！ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 例題だけはヤメろ！『１対１対応の演習』を吸い尽くす使い方＆レベル！ […]
すみません。ふと疑問に思ったんですけど、基礎問題精講に書いてあることを100%マスターできれば、東大理系でも半分は取れるんですか？
理論上は無理かもしれませんけど、絶対無理というわけでもないんじゃないかと思ったので、質問しました。
考え方としては１つの知識をどれほど拡張・応用できるか、という能力を「地頭」と呼ぶなら、その地頭によります。めちゃめちゃ地頭いいなら、別に試験中に公式を全部作り出してしまえばいい話で、そうすれば基礎問題精講を一切やってなくても理論上満点がとれます。逆に一切他の問題に応用できないような地頭なら、基礎問題精講をやっても、その数字変え問題くらいしか解けません。っていう考え方でやってます。
京大文系志望の自称進の高二です
今年の3月から始めて5月までは数lAに全振りしていたのですが、現在はllBと並行で進めており、lA:llB=6:4くらいの割合でやっています。
lA基礎問題精講は6周と苦手なところを1周し、ある程度解ける気でいるのですがまだ苦手な分野(二次関数、データの分析)に不安があります。センター過去問数lAで7割とれました。
llB基礎問題精講は現在学校で習った範囲を進めているところです。
夏休みまでにはlAを終わらせておきたいのですが、今のペースで進めても極まる気がしません。夏休み前まで数lAに全振りして、夏休みから数llBに移行した方が良いのでしょうか?
また、いつまでにllB基礎問題精講を終わらせればよいでしょうか?
拙い文章ですみませんお返事お願いします
いったん1aに全振りするのはありです。本来6周してるならセンターで8,9割は解けるようになっておきたいところです。
１対１を高3夏までに終えておけばよいので、今年中に2bの基礎問題精講を終わらせれば最悪大丈夫です。
分かりました。危機感が半端じゃないので、焦らず進めていこうと思います。
こんばんは。2年前ほどから拝見していました。相談のコメントを失礼します。偏差値66くらいの高校から通信制に転学した現在高2(新高3)で、熊本大学医学部医学科志望です。10月の駿台模試で数学が偏差値65.3国語が53.7、英語が63.2でした。これまでしま勉強として数学は基礎問→一対一(2Bまで終了)、英語は総合英語beと入門英文法問題精講+シス単+鉄壁を2週、東進レベル別3、4を無理やり解いた、国語はなにもしていません。理科社会はほとんど手をつけていないのですが、今からやって間に合うでしょうか。また国数英も医学部志望としてはかなり弱いと感じていますが、特に英語が正直中学時代全国レベルだった名残でこの成績がとれてるだけでほとんど勉強したことがなく勉強法が確立していないので伸び悩みそうです。数学は数3をやりつつ1A2Bのプラチカをやっています。国語は正直よく分かりません。。アドバイスお願いいたします。
数学は達成した参考書と成績を見る限り特に問題なく順調に進んでいると思います。そのままの勉強法で進めてみてください。
英語はテコ入れとして英文解釈の参考書を入れてみると一気に伸びる感じがしますね。絶対じゃないですが、割といい影響は出ると思うのでおすすめです。
国語は放置でいいです。正直直前に古典やるのが一番コスパいいので、致命的でなければ放置しといてください。ヤバそうなら林修受けてみてください。
社会も倫政もしくは地理選択なら直前3ヶ月までは無視でいいです。
理科は普通に間に合わなそうですね。とりあえず数英メインで伸ばしながら、教科書レベル+αまで完璧にしときたいです。そしたら現役でも十分チャンスはあるし、浪人しても確実です。
お忙しい中返信ありがとうございます。理科はとりあえず化学→リードα、物理→スタサプ＋リードα(一応)で進めていきます。社会は倫理を選択しようと思ってます。一浪まではギリギリ許されるので、頑張ってみます
コメント失礼します。
現在数3基礎問題精講をやっているものです。インプットが終わってないのでアウトプットと同時並行でやっており、12月中旬には1周終わってると思います。
Dioさんのスタプラのアカウントを見てみると基礎問題精講を2ヶ月、約68時間で終わらせていました。
7周するのにこの速さだったのは何か理由があると思いますか？
単純に学校の内職の分などを記録していなかったからかもしれませんがよければ教えてください。
単純に学校の内職の分などを記録していなかったからかもしれませんが
→それは大きいですね。純粋に時間をすべて計ったのは数3の基礎問題精講だけですね（基礎問シリーズでは）。だからそっちのほうが参考になるかもしれません。
7周するのにこの速さだったのは何か理由があると思いますか？
→解けないことに一切の躊躇を抱かなかったことですかね。本当に毎日ノルマをこなすために爆速で周回しつつ要点は毎度抑える。っていうそのバランスが奇跡的だったんだと思います。
高二電通大志望です。
数学は今まで10日あればいいを使っていたのですが今からでも基礎問に変えた方がいいのでしょうか？
このあともう1段階上の参考書に移行する予定があるならそのままやればいいと思います。ただ、10日あればいいだけで受験するつもりなら、基礎問に変えたほうがいいです。
高一東大理系志望です。アドバイスを頂きたいです。僕は、数学がかなり苦手なので入門問題精講を使って勉強しています。校内のテストでは平均ぐらいでとても焦っています。学校のテストには青チャートや4STEPから問題が出て、青チャートは宿題にもなります。僕としては教材をある程度絞って勉強したいと思い基礎問を使っています（チャートや4STEPはバツトキ）。ここで3つ質問があります。1、基礎問はやめてチャートとかに絞るべきなのか。
2、4STEPの内容は教科書＋チャートでカバーできるのか。そうでなければ演習量を稼ぐ＋テストで高得点をとる、という意味で4STEPをするのとテストにとらわれずどんどん先へ進むのとではどちらがいいのか。
3、独学する時には効率重視で入門→網羅系→1対1と行くか、どうせやるので教科書を入門の次にやるのとではどちらがいいか。
勉強法が確立できておらず、自分に何が足りなくて何を優先させればいいのかがわからないです。質問内容も具体的すぎると感じていて根本的な内容を質問できていないことをお許しください。dio様の意見を聞きたいです。
2.4stepではチャートの難しい方の問題はカバーできません。テストにとらわれずもっと先を見据えて勉強すべき。別に受験に受かれば他はどうでもいいはずです。
3.教科書をやる意味は正直わかりかねるので、効率重視でいいと思います。
お忙しい中ありがとうございます。追加なんですが、高3までには、英語の文法や解釈などと数学の1対1レベルをやるのとではどちらを優先させるべきでしょうか。
どっちもです。その2つは最低限終わっているべきです。理科も国語もあるということをわすれないでください。
こんにちは。高校2年生です。
この夏休みに数3基礎問題精講をやろうと思い立ち、どのくらいで終わらせるのかの目安にしようと思ってdioさんのスタプラのアカウントを見ていたのですが数3基礎問は合計68時間ほどでした。
今まで数2bまではチャート式しかやったことがなくて、どれも4、5周はしていたのですが(完璧になるまで)200時間(？)くらいはかかっていたような気がしてます。
これはdio さんの処理能力の高さ故なのか基礎問題精講とチャート式の違いなのかで少し困惑してます。自分も70時間かからず終わるのなら願ったり叶ったりなのですがdioさんはどう思われるか教えて欲しいです。(計画を立てるための参考にしたいので)
どっちもですね。数3の基礎門をやってたときは、既に1a2bが完成していて計算力も高かったです。そのうえで問題数も絞られていたので、毎日例題1周とかのペースで解いてた気がします。まあ、140時間みておけば必ず7周は終わると思います。
問題数も絞られていた
とはどういうことですか？
高1理系です。
基礎問題精講を数学3まで進めるのと、基礎問題精講1Aが終わったら、1対1対応に進むのはどちらがよいですか？
前者です。
筑波大志望の高1です。基礎問題精構について、今後の予定を立てているのですが、回答をお願いします。基礎問題精構は、解説が分かりやすいですか？わからない時の対処法として①スタサプを見る②初めから始める数学を使う③youtubeで解説を探す④学校の先生に聞く の四つを考えています。どれがベストな選択肢でしょうか？また、確認ですが、基礎問題精構を極めれば青チャートは必要ないということでしょうか。なるべく早めに進めたいので、できれば基礎問題精構だけで基礎は固めていきたいと思っています。
基礎問題精構は、解説が分かりやすいですか？
→特別わかりやすくもわかりにくくもないです。人によって向き不向きもあるので、不安なら書店で見るのが一番いいです。
どれがベストな選択肢でしょうか？
→どれもベストになりうります。単発の疑問は③④、大規模な疑問（単元そのものがよくわからない）は①②③を使うべき。
基礎問題精構を極めれば青チャートは必要ないということでしょうか。
→基礎問題精講と一対一の2つを使うことで青チャートを完全に網羅できます。MARCHまでなら基礎問題精講のみで十分です。
ありがとうございました。
すみません。もう一つ質問させてください。基礎問題精構を極めたら数字を変えた類題は解けるようになるとは思いますが、共通テストはそういう類題が多いということでしょうか？もしそうでなければ、これとこれの問題の組み合わせだなと気付けるようになるために何をすればいいですか？
共通テストはそういう類題が多いということでしょうか？
→基本そうです。
これとこれの問題の組み合わせだなと気付けるようになるために何をすればいいですか？
→何周もして体で覚えれば、気付く気付かないにかかわらず手が動きます。
基礎問題精巧を極めたら一対一は初見でどのくらい解けますか？
6,7割くらいが正常でしょう。
すいません。他のコメントを見たので基礎問はチャートに 絞ります。
白チャートからの接続は良いですか？
標問や一対一に行くのは不安なので、基礎問を挟もうと思っています。
基礎問は白チャートとかなり被るので接続は悪いです。そのまま一対一に行っても何とかなると思いますよ。
そうなんですね！！
一対一行きます！
網羅系の参考書をやったのに共通テストでそれに見合う点数が取れません。河合塾の記述模試ではなんか見たことあるような問題だなぁ、とかあの解放使えそうだな〜、とかで解きやすいんですけど、共通テストになって誘導があると何それ！？ってなって全然解けないです。基本的に網羅系の例題を最初に解いた時は全然わからなかったので、考える時間はあまり作らずこんな感じかーって答え見てたんですけどそれが原因で初見の問題に対応できてないかもしれないです。何か対策ありますか？
とりま無視して突き進めばいいんじゃないでしょうか。河合の方はできてるなら、基礎力はついてるわけで、あとは慣れとか初見への対応力が上がれば勝手にできるようになると思います。
今、偏差値５９の中高一貫校に通っている高校１年生です。志望は旧帝の理系学部です。自分の通っている高校は旧帝の合格者は毎年数名ほどですが、２個上の先輩が東大レベルで憧れています。しかし、自分は直近の東進模試で数学偏差値５４と志望とかけ離れています。今、自分の計画では基礎問題精講の数IとAを３ヶ月くらいで解きまくり、完璧にして年末までに１対１も完璧にしたいと思っています。この計画に問題があったら、教えてください。またその後取り組むべき参考書も教えてください。
次に英語ですが、文法のポラリス１を購入しようと考えているのですが、他にいい参考書がありますか？ 単語はCASIOの電子辞書の教材を使用しています。長文失礼しました。
とりあえずその計画でいんじゃないですか。その後取り組むべき参考書っていっても、さっさと2b3cを終わらせないと何も始まらないんで。そこらへんを1aと同じように進めるしかないでしょう。
サラッと文法をさらうだけならBest400とかの方がおすすめですが、正直どれでやっても分量以外は大差ないです。
現在、中高一貫校に通う高校1年生です。中3の時には数IとAは9割ほど終わりました。志望校は旧帝の理系学部です。今、数IとAの復習をしようと思うのですが、青チャートと基礎問題精講で迷っています。数学は好きな教科ですが、青チャートの暑さにはビックリしました。dioさんの意見を教えてください。
また、英語の文法の参考書では、castdise TVの動画を参考にポラリス1を使用しようと思うのですが、ほかにオススメの参考書が有れば、教えてください。文法以外の参考書もぜひお願いします。
私は、あの厚さに耐えきれないなら基礎問題精講一択だと思いますよ。Best400とかはおすすめ。文法以外の参考書も記事だしてるんで、そちらを参考にしてください。
千葉医志望の高3です。
基礎問の演習題をやらないという選択肢はあるでしょうか？
DIO様の記事は何十回も読んでおり、DIO様が演習題も解けというスタンスを取っている事は知っていますが、武田塾など、他のサイトでは基礎問の演習題はやらなくていいとあり、僕自身時間が全然足りないのでやらなくていいなら飛ばしたいと思っています。
基礎問の精講に演習題の番号が振られてることからも演習題をやった方がいいのかなと思っていて、とても悩んでいます。
このブログでは、特別な才能や環境を持たない普通の学生に当てはまる方針を提示しています。だから、別に特別な事情があれば、他の選択肢を取ることもあり得ます。数学的なセンスがある人ほど少ないインプットで、より多くの問題にその知識を活かせます。基礎問の例題のインプットだけで共テ８割を超えるようであれば、演習題は解かなくてもいいです。ただ普通は、インプットの量を増やしたり、アウトプットの練習をしないと、いい点数にならないので、演習題も薦めています。
ちなみに時間がないなら現役は諦める方が結果効率が良かったります。私の親友の一人も千葉医志望でしたが、途中で間に合わないことを悟って現役時は基礎固めに集中してました。まあ何を選ぶかはお任せします。
はじめまして。
網羅系問題集をかけられるなすことの必要を感じ、この記事に辿り着きました。
現在1Aの例題3周こなしたところなのですが、全て記述してこなしているとそろそろスピードの限界を感じています。
数学に限らないことですが、よく聞く「読むだけ」の効果は実際どの程度の効果があるのでしょうか？
私は読むだけで成績が上がるのは、もともと並外れた計算力を持っている人に限ると思っています。ルールを理解しただけではサッカーが上手くならないのと同じで、実際にやってみることで処理力（共テが好きなやつ）は磨かれます。
ふたたびの質問失礼します。
記述してこなす中で、基礎問題精講の解答をどの程度厳密に再現するのがよいでしょうか？現在、サイコロ１つ転がすのに同様な確からしさを確認し、一色の場合を足すのにも分かりきっていようと排反であることを書いて確かめるように意識しています。基礎問題精講からこのような意識でこなすのと、記述の練習は1対1から練習するくらいに割り切ってしまうのとではどちらが混乱を生じないでしょうか？
一対一をやらずにスタ演だけ何周もやっても一対一を何周もしたのと同じくらいの実力はつきますか？
普通の人なら絶対につきません。それなら一対一を何周もやったほうが、点数高くなります。
スタ演が最初からある程度解ける状態だとした場合もですか？
それなら話は別ですが、一対一レベルが完璧でないなら後々伸び悩むことになります。
コメント失礼します
基礎問題精巧の使い方についてなのですが、間違った問題は印を付ける程度にし、間違えなくなるまで繰り返さずに周回を先にするべきでしょうか。
私はいつも一周した後に間違いを潰してから二周目に入るのですが、その方法は時間がかかり過ぎて周回が疎かになってしまいます。
間違えなくなるまで繰り返さずに周回を先にするべきでしょうか。
→はい。よっぽどわからないやつなら別ですが、基本は周回しているうちにできるようになります。
こんにちは。
基礎問題精巧を何周も何周もして、
極めたのですが共通テストの過去問
を解く時上手く利用できず
全然点数が取れません。何が原因ですかね
極めたつもりになっだけで無意識のうちに
答えを覚えてしまってるんでしょうか？
何周もしてるうちに答えだんだん答えを
覚えてしまうと思うのですがdioさんは
そことどう向き合ってましたか？
また、センターの模試の前に基礎問題精巧
の他に何かやりましたか？過去問、ほかの参考書など…ご教示して下さると幸いですm(_ _)m
私は毎回初見のように7周したらできるようになりました。私は偏差値70を超えたときには基礎問題精講しか使ってませんでした。
一つ可能性があるとすれば、共通テストになってから、特に大問1・2は切り口が独特な気がしています。その独特な雰囲気に対応できずに、点数が伸びないという可能性はありますね。一度センター試験の過去問を解いてみて、9割を超えたら自信を持って次の参考書に進んでいいと思います。それでダメなら、また原因を考えましょう。
コメント失礼します。
高３第1回駿台全国模試は一対一対応を完璧にしたら150点普通に取れると書いてある生地があったのですがそれは去年の駿台全国模試が簡単だったからですか？それとも毎年第1回はそのレベルですか？過去問を手に入れる手段があまりないので参考にしたいです。
毎年難易度としてはそんなもんです。一対一の知識があれば、解説を見て「あーなんだそんだけか」ってなる問題は150点分以上あると分析しています。
新スタンダード演習や優しい理系数学まで
やらなくても一対一を漏れなく完璧にしていたら150取れるんですか？！
取れますよ。私の友達は一対一直後の模試で、184点取って全国一位でした。
返信ありがとうございます！184点で全国一位と言うのは数学は184点であと総合が1位だったということですか？
それともう1つお聞きしたいのですがどうしたら朝早く起きて勉強出来ますか？泣朝早く起きるためにしていたことはありますか
dioさんが188点で27位って記事あるので184で全国1位じゃなくないですか？😓なんかLINE感覚で返信沢山してしまいすみません笑なかなか勉強について聞ける人が周りにいなくて…笑
いや確か数学で一位だしてた気がします。私は基本9時〜9時30分の間に寝るようにしてました。
じゃあ違う模試だったんじゃないですかね。
そうなんですね。どちらにせよとりあえず基礎問題精講と一対一対応完璧にしたら150いくということですね？それと頻出問題や苦手な単元以外の重点的に勉強した方がよい単元を教えてもらえると幸いです。
ゴールは駿台模試じゃないと分かっているのですがどうしても数学良い点数取りたくて…
別に参考書をやったら自動的にその成績になるわけではないです。「凡人でも工夫次第で、理論上150点くらいなら行けるよね」っていう目安なので、そこは勘違いしないで頂きたい。一部分を重点的にやるより、全体的に万遍なくやる方が点数は高くなりそうです。
こんばんは。コメント失礼いたします。
基礎問題精講の中でも特に大切な問題を教えていただけますでしょうか。
よろしくお願いいたします。
全部大切です。強いて言うとかもないです。どの問題もできないと失点に直結します。
2022年度から指導要領が改訂され、数Cが追加されます。まだ新課程に対応した基礎問題精講が出ていません。ⅠAとⅡBは改定前と変わらないので、最悪の場合、ⅠAⅡBは基礎問題精講、ⅢCだけ青チャートというのでも大丈夫でしょうか。新高一です。
全然いいんじゃないですか。3cは割と計算力重視の面もあるんで、青チャートでも十分良いと思います。
それか3cが改定とはいっても、1a2b3c全体で見たとき、たしか行列分野が移動するだけだったはず。なので、何なら旧課程版で基礎問題精講をやって、データの分析の上位互換の単元は基礎問題精講に入ってないので、そこだけ別途「面白いほど」とかで補えば十分なんじゃないかなとも思います。
現在、京大医学部を目指している高1です。
煽チャートをやっていましたが、問題量が多く挫折しました。そこで、基礎問題精巧をしようと思いましたが、自分は、東進共通テスト模試で数ⅠAが16点でした。今まで演習せず、適当に学習してきた結果です。学校ではももう数ⅠAが終わっています。基礎問題精巧対象者として、センター３割：理解力に自信があればどうぞ
それ以下：「とってもやさしい数学」からと書いてありますが、やっても大丈夫でしょうか？もし無理なら、何をどのようにどのくらいの期間で行えば良いですか？
↓基礎問題精巧をすると仮定した時のルート
2月～3月 基礎問題精数ⅠA
4月～5月 基礎問題精巧2B
6月～7月 基礎問題精巧Ⅲ
8月～9月 1体1の1A
10月～11月 1体1の2B
12月～1月 1体1のⅢ
あと、参考書付け足して、過去問
のように自分は、計画を立てました。この計画で問題点・改善点など教えて下さい。また、この計画では、医学部では遅いでしょうか？自分としては、基礎問題成功と一対1対応をもう少し早く終わらせたいなと思っているのですが速さ的にはどう思いますか？それとこの計画よりも早く終わるさせるためにはどうしたらいいですか、り、そのルートなど教えて欲しいです。
私は、東進に通っていて、基礎問題精巧を進め方として、
東進の受講して、教科書読む→基礎問題精巧
と考えています。大丈夫でしょうか？
また、１日、何問のペースで進めていくと良いでしょうか？
少し気になっていることで、東大理IIIは、地頭や才能であり、一般人には無理でしょうか？本当に夢みたいですが、今から頑張って東大理III行けるかな…🤔と思っています。考えを聞きたいです。
質問が長くなりましたが返信よろしくお願いいたします🙇♀️
「とってもやさしい数学」からと書いてありますが、やっても大丈夫でしょうか？
→基本的にはやっちゃ駄目だから、まあこう書いてるわけですね。基礎問題精講の解説を理解できる自信があれば、やってもいいです。あと現役で離散を狙うなら、まあやるしかないです。ただそこそこ厳しいとは思います。
この計画で問題点・改善点など教えて下さい。
→全部1.5倍して高3夏の手前まで一対一にしましょうか。応用は最悪一冊で終わらせて、数学は必要最低限取るのが得策だと思います。下手に基礎を急いで、結局穴だらけになるのが一番ヤバイです。
１日、何問のペースで進めていくと良いでしょうか？
→20問くらいやらないと間に合いません。
最後に一つ言っておくと、離散や京大医学部志望は、高1の終わりで数学は割と出来上がってます。つまり一対一レベルはだいたい仕上がってます。もしくは英語がキチガイです。そのうえで、高2は理科を詰めていきます。才能以前に、受験に対する準備量が圧倒的に違います。だから、本当に離散に行きたいなら、最初から浪人覚悟で、基礎からミッチリやる計画を立てた方が、変に焦って現役を狙うより、格段に合格率は上がります。
現在高一の地方自称進学校に通っているものです。
今数学の先取りをしていて数２まで、青チャートの例題が2周（微積は1周、数１はもっとしてると思います）終わっています。1対1の数一とハッと目覚める確率を解いたところで受けた駿台模試の得点は151点でした。正直1体1で点が伸びたと思います。なので早く1対1に入りたいのですが、このまま青チャートを続けるのか、それとも基礎問題精講をするのかどちらがいいと思いますか？なるべく一年生のうちに数2Bを終わらせたいです。
2周しているなら、青チャートを続けるほうがいいでしょう。一対一に意識が向いて青チャートが疎かになると、思わぬところで足をすくわれかねないので、丁寧に行きましょう。急いで基礎がユルユルで高3になって返ってくるくらいなら、遅くても基礎をガチガチに固めた方が圧倒的にメリットが多いことは意識しておいてください。特にまだ高1ですので。
高２名大理系志望です。
高1の時から青チャートを定期テストの範囲の所をそのテスト期間の時だけ2,3回解いてきました。
あと1年しかない中でで少しだけ手をつけた青チャートを何周もするかどうか悩んでいます。
それとも、基礎問題精講,標準問題精巧などの薄めの参考書からプラチカ,やさ理につなぐべきでしょうか。
河合の全統の数学偏差値は65でした。(高２の5月のもの)
模試の結果からするとそこそこに基礎はできているので、青チャートをこのまま周回した方が良さそうですね。今から基礎問題精講にいくと非常に退屈かつ無駄を感じると思います。私が薄めの参考書をすすめるのは、0から青チャを進めるのは非効率だから。もしある程度基礎が入っているなら、青チャートでも全然いいと思います。
アドバイスありがとうございます!
これから青チャートを何周もしようと思います!!
何度もすみません。
名大理系数学はやさ理などの間に一対一を挟むべきでしょうか。
また、受験までの青チャートの理想的な終わり方や他の参考書の入り方もよければ教えて頂きたいです。
高一東大志望です。
基礎問題精講と一対一でフォーカスゴールドなどの網羅度はカバーできるのでしょうか？
周りがフォーカスゴールドを使っていて不安になってしまいます。
全然カバーできます。そこは安心してください。むしろfgから一対一に行く人も多く、だいたいみんな時間を無駄にすることになります。東大入試は倍率3倍なので、周りと同じことをしない方が合格可能性は高いとも言えますね。
高校2年の慶應義塾理工学部志望です。
進研模試の4月の数学の偏差値は62。河合塾の全統模試は53でした。
現在数学の基礎固めとしてサクシードと教科書を併用してやってるんですが、その後に基礎問題精講をやろうとしているのですが大丈夫でしょうか？
全然大丈夫だと思います。ただ残り時間がどうなのかは微妙ですが。
お忙しいところ失礼します。
基礎門は例題だけ周回して次に移ってもよいでしょうか。
それともやはり演習問題まで解いたほうが良いのでしょうか。
回答よろしくお願いします。
いいか悪いかで言ったら、当然演習題も解くべきです。そんなことは当たり前なんで、聞いてないのはわかってます。
一応目安としては、例題だけやって、共通テスト型の模試で8割を超えているなら演習題は自信を持って切り捨てて大丈夫です。7割前後なら、残り時間と要相談。6割台もしくはそれ以下なら、もっとちゃんと例題も演習題もやってください。近いうちに模試がなければ、センター試験の過去問をネットで拾って解いて確かめてください。
了解です。ありがとうございました！
コメント失礼します！
自分は現在中高一貫校（公立で進学校では全然ないです）に通う中2です！
僭越ながら,志望校は東京大学の理科三類をめざしています！
自分の進度としましては現在時点で数検、英検ともに2級を所持している状態で、
この記事にもあるように基礎問題精講を瞬殺できるようになろうと周回しているところです！
数学Ⅰから数Ⅲまでとりあえず一通りおわったのですが今後の学習で意識した方が良い点や行った方がよいことはありますか？
また、進度としては遅い（足りない）でしょうか？
長くなってしまいましたがご意見、アドバイスを頂けると幸いです。
意識した方がいいこととして、自分なりの勉強理論を組み立てていくことです。もしかすると、もうでき始めているかもしれません。実績に裏打ちされた勉強法を確立していくと高学年になっても戦っていけます。それと、ただ先取りしてるから成績がいいだけ、という状態にならないように細心の注意を払いましょう。
進度としてはバリ速いです。私が基礎問題精講を終わらせたのが中2の冬だったので、相当です。そのままペースを崩さず行ければ間違いないです。頑張ってください。
アドバイスありがとうございます。
頑張ります！
また困ったことがあれば質問させていただくこともあるかもしれませんが、
よろしくお願いします！
こんばんは、京大文系志望の地方公立高校の高1です。まだ数学は1A、微積、三角関数程度しか履修していません。
学校が進研模試を取っているのであまり参考にならないと思いますが、一応数学の進研模試での偏差値は75です。学校の定期テストでは1Aどちらも90点程でした。
質問なのですが、学校がフォーカスゴールドを勧めていて、フォーカスをやるべきか、基礎問題精講をやるべきか、それとも標準問題精講をやるべきか迷っています。
フォーカスは学校の指定している型の一個前の版を何故か持っているので、正直課題の範囲すら違ってまともに使えていません（一応履修済みの範囲の難易度星3.星4は例題と問題どちらも全て解きました）。
基礎問題精講、標準問題精講、フォーカスのどれをやるのがいいのでしょうか？またその場合どのように周回するとよろしいでしょうか？自分の客観的なレベルがよく分からないのでアドバイスお願いします。
私も進研模試の詳細がよくわからないのでなんとも言えませんが、多分基礎はできてそうです。高1ということですので、多分そのままFGを進めるのが一番いいと思います。FGの星4はかなり難しい問題も混ざっているので、まずは星3までを周回して完璧にしましょう。時間があれば星4も勉強するといいと思います。
ありがとうございます。
FGについては別の記事にあった通りに周回したいと思います。ただ、例題を見ただけですぐに解法がわかるようなものは飛ばしてもいいですか？
飛ばしてもいいですけど、そこは自分に厳しくしてくださいね。あんま飛ばしてばっかりいると計算力が伸びませんから。
はじめまして。千葉大法政経学部志望の者ですが基礎問題精講のあとにやる参考書・問題集は何がいいでしょうか？
一対一へ進んで過去問が妥当だと思います。
千葉大文系に標準問題精講はオーバーワークでしょうか？
それでも問題ないです。
東北大理学部希望の高2です。
数学1A２Aについて、青チャートで共通模試85%取れました。9割取れたら、キャンパス→過去問で大丈夫でしょうか？
大丈夫だと思います
こんにちは。現在高校三年生の者です。
基礎門と青チャートを併用して使っていますが、効率が悪くないかと不安です。
５月から2ヶ月程で基礎問1A 2Bを例題のみ2周して、青チャートを解いています。青チャートは大体一週間で例題を一周できるペースです。
志望大学は名古屋工業大学（地方国立〜）です。
５月に受けた河合模試での数学の偏差値は45でした。最終的に数学偏差値65程は安定して取れるようにしたいです。
数学の勉強のアドバイスお願いしますm(_ _)m
基礎問と青チャートが終わったら、やさしい理系数学か、一対一をやろうと思ってます。
これから青チャートの周回に力を入れて、夏休み明け頃に偏差値が65弱までいけば、やさ理。偏差値が60前後なら一対一にするのがいいと思います。ちなみに60前後までは青チャートの例題で頑張ってください。私なら夏休みの青チャートの出来で、計画を組み替えていきますね。
はじはじが終わって元気が出る数学をしようと思ったんですけど、基礎問題精巧の方が良いですかね？高2で模試の偏差値は50です。
ぽぽぽさんコメントありがとうございます。
正直どっちでもいいですけど、自信がないなら基礎問題精講の方がいいかもしれないですね。私も基礎問題精講でやりましたし。
長崎大学医学部志望の者です。
数学の参考書について相談です。
今黄チャートを進めていてこの後自分では駿台のcanpassか河合塾のチョイスかで迷っています。アドバイスお願いします。
また、これらよりおすすめの参考書があればそちらも伺えればと思います。
お忙しいとは思いますがよろしくお願いします。
あるさんコメントありがとうございます。
長崎大医学部志望とうことでしたら、チョイスでは物足りないです。キャンパスか一対一に進むといいと思います。
現在高1です。度々質問申し訳ないです。
dioさんのルートは本当によく練られていて参考になりました！これからも基礎問と一対一でゴリゴリ進めていこうと思うのですが、青チャやfocusは解法辞書用として持っておいた方が良いですかね？次のステップ（やさ理など）に進んだ時にそういったものが必要かどうか教えて頂けると嬉しいです。よろしくお願いします！
正直いらないです。私はそんな用途で使ったことはありません。
了解です！ありがとございます！
こんにちは。高2です。
dioさんが基礎問題精講をやった際のやり方に
質問なんですが、
5日間解いて2日間復習など、復習の日を設けましたか？それとも復習の日を設けずにひたすら
周回しましたか？
回答お願いします。
こんにちは。高2です。
dioさんがをやった際のやり方に
質問なんですが、
5日間解いて2日間復習など、復習の日を設けましたか？それとも復習の日を設けずにひたすら
周回しましたか？
回答いただけたら嬉しいです😆
こんにちは。高2です。
dioさんがをやった際のやり方に
質問なんですが、
月曜から金曜まで解き進めて土日に復習など、復習の日を設けましたか？それとも復習の日を設けずにひたすら周回しましたか？
回答いただけたら嬉しいです。
後者のひたすら周回でした。
ごちゃごちゃコメント送って
しまって申し訳ないです。
本当に聞きたかったのは
周回方法の質問でしたが、
面白い回答も含めて返信ありがとうございました😊
とにかく基礎問題精講
何周もします❗️
私は本当にただ永遠に周回するだけでしたよ。毎日同じことを繰り返す方が性にあってたので。ときには脳筋になるのも大事です。
こんにちは。とても参考になりました。
こんにちは。
がんばります。
好きな食べ物教えてください
女のコです。
学校で配られる教科書傍用問題集(4stepなど)とこの基礎問題精講のレベルは同じくらいですか？
シュークリームさんコメントありがとうございます。
だいたい同じですね。
ありがとうございます。
学校で4stepを配られ、定期テスト対策にはこれを使えと言われたのですが、問題数が多いので基礎問を何周かする方がいいと思い基礎問で対策を進めているのですが、網羅度などは大丈夫でしょうか？
全然大丈夫です。むしろ良問に絞ってあって効率的です。
何度もありがとうございます。
基礎問題精講を頑張ろうと思います。
こんばんは、質問させてください
学校行ってないので基礎0です、今は偏差値48程度の摂南大学を目指してます
スタディサプリスタンダード→白チャートのコンパス3まで解いてからその単元の基礎問題精講やってるのですが問題が難しいです
例えば二重根号を外すなんて白チャートだとコンパス4ですしスタディサプリでは習ってないです（youtubeで解説を見ながら解きました）
この場合なにか他にするべきか、チャート式でコンパス4レベルを終わらせてからやった方がいいのでしょうか？
それとも基礎問題精講に入る前になにか違うのをやった方がいいのでしょうか？
白チャートやスタディサプリで扱わなかった問題は解説も理解出来ずに一人で何十分も悩んで大抵はyoutubeで理解して復習するのですが次の日には忘れてまた復習しています
というか普通の人は解説を見て、理解して先に進めるのでしょうか・・・？
見てたらでいいので何個も質問してしまいましたがよければ返信お願いします
やる気元気さんコメントありがとうございます。
おそらく学校に行ってないのがそこそこ効いてますね。まずはスタサプとyoutubeを使いながら白チャートの例題を全問完璧にしましょう。基礎問題精講は一旦封印します。
わからない問題があればすぐに答えを見て、映像授業を見て、理解してください。下手に長時間考えると体力だけ吸い取られて何も残りません。
普通の人はある程度「そういうものなんだ」と割り切って理解を諦めている場合が多いように感じますね。正直大学受験はそれで攻略できるので、そういう割り切りの心も必要なのかもしれません。
数学で「この解法どうやっても初見じゃ思いつかないだろ」みたいな問題ありませんでしたか？私はたまにあるのですが、その問題は暗記する感じでいいですか？
データらぼっちさんコメントありがとうございます。
ありましたね。まあたまになら暗記しちゃって大丈夫でしょう。私も暗記した問題が何個かあります。
チャート式が合わず、トライしてみました。
手っ取り早く復習&入試基礎固めができて、なかなか良い参考書かなぁと思います。
「確率の最大値」のような、チャート☆5クラスが、見開き1ページの解説で済まされているなど、設問によっては解説ページ数の縛りがきついかも、というものもありましたが。
青チャートは「例題」の計算や式変形もレベルが高いことが多く、
なぜそうするのかというヒントなり、「ここは定石だから覚える」なのか否かがあまり書いていないですよね。
また「例題」に対して「練習」が骨がありすぎ、式変形などの攻め方も例題と違ったりして、
パターンを身につけたいのに全然進まない教材でした。
難関なら青チャートの単元学習が土台として必要だ、とは言われますが、
青チャートが自分でこなせる人はもはやどの教材でも結果を出せると思う！ので、
有名な割には万人受けしない教材のはずなのに、なんでみんな買うんだろう？ と思ってます。
数学勉強し直し中の人さんコメントありがとうございます。
本当にその通りだと思います。
今年から偏差値68くらいの高校に進学する新高一です。
一応京大の理系に行きたいと考えていて学校の進度では足りないと思うので高二の12月くらいには数ⅢCまで終わらせようと思っています。
そこでdioさんの記事を拝見して、FGの例題部分と基礎問題精講を自分で比較してみたんですがFGの方が解説が詳しく網羅性も高いと感じたのでそちらを使いたいと考えています。
まず4ヶ月ほどで数ⅠAのFGの例題+練習を最低三周してその後一対一を二ヶ月ほど二～三周で合わせてという感じ各半年ずつで進めていくつもりなのですがこれの改善点はありますでしょうか？
またやさ理などは三年生になってからやろうと思っていますがそれで問題ないでしょうか？
長文になってしまって申し訳ないですが回答いただけると嬉しいです。
新高1さんコメントありがとうございます。
改善点はありますでしょうか？
→大変いい計画だと思います。勉強法は千差万別なので改善点というわけではないですが、私ならもう少し周回数を増やします。もちろん模試の成績で判断していくわけですが、基礎レベルの問題は「ただ解ける」だけでなく、「条件反射的に解ける」状態まで持っていくことが重要です。多少無駄だと思ってもある程度の演習は我慢した方が（特に共通テストで）有利に働きます。
またやさ理などは三年生になってからやろうと思っていますがそれで問題ないでしょうか？
→問題ないと思います。高3から始めると応用系の問題集は3冊前後で、十分な演習を確保できると思います。
新高2です。質問なのですが、dioさんは青チャートもやられたそうですが基礎問＋一対一と青チャートで網羅度に差はあると思いますか？解いた感想を教えて頂けると嬉しいです。よろしくお願いします！
baseballさんコメントありがとうございます。
私個人の感想では、青チャートの例題と基礎問＋一対一の間に網羅度の差は全く無いです。どちらを選んでも到達点は同じですし、対応力も同じくらいになります。ただ友達の話を聞いていると青チャートより一対一で才能が開花する人が多いです。
ありがとうございます！
ありがとうございます！がんばります！
質問させていただきます。
新中3です。単純に言うと、共通テスト本番レベル模試の点数を上げたいです
現在共通テスト本番レベル模試で1A65、2B40(換算得点50弱)です。
それぞれほとんど手を付けていない基礎問とFGがあるのですがそれぞれどちらを使えば良いでしょうか？
また、基礎問の後にFGをやるのはありでしょうか？
最後に、「例題と演習を交互に」と言うのは具体的にどう言う意味でしょうか
質問多くてすみません。
基礎力つけたいさんコメントありがとうございます。
数2bは確実に基礎問をやるべきです。数1aはどっちでもいいですが、時間もありそうですし、fgでいいと思います。
別にナシではないですが、それなら一対一に進んでいいと思います。あとで弱いなと思ったところはfgで演習するとか、そんな使い方でいいと思います。ただやりたいなら、別に止める理由もないです。まだ新中3ということなので、自分の直感を信じて試行錯誤しながら勉強法を確立するのがいいと思います。自分なりの勉強法があると高2高3でメチャクチャ強いです。
例題を一周して、演習を一周して、例題を……ということです。
現在高2(新高3)で、現在、東北大学医学部志望(自分の興味関心が変化すれば志望校変更の可能性大)の者です。
数学
全範囲終わっています。
学校ではFocusGoldを配布されました。
IA IIB→夏休み中に全問一回解きましたが、問題数が多すぎてその後継続することを挫折。その後放置してしまいました。正直もう使いたくないレベルです。共通テスト体験はIA43点ⅡB62点でした。
lll→あまり演習していません。
この場合どんな問題集から始めて、それをいつぐらいまでにどのくらいやって、終わらせて次の問題集に行くべきでしょうか？
それから、考えてわからなかった時に解答を見るタイミングはどのくらいでしょうか？
化学
そろそろ終わります。
学校ではセミナーを配布されています。
セミナーはまだ完璧ではないです。
セミナーもしくは他の同じレベルの問題集をいつまでに何回回して次の問題集に移るべきでしょうか。
物理
おそらく前の範囲をほとんど忘れていてほぼ一からやり直す感じです。センサー物理、漆原の明快解法講座を持っています。
どこからどう始め、いつまでに終わらせれば良いでしょうか。
英語
共通テストはリーディング75点、リスニング82点でした。文法がからっきしで学校ではupgradeが配られています。まだ半分くらいしか解いていないです。単語はシスタンを使用しています。いつまでにupgradeを何回ぐらい回して他の文法問題集に移るべきでしょうか。
また、ほかに英語の勉強でやっておくべきことはありますか？(ほかに速読英単語必修、上級編、evergreen を持っています。)
量が多くてすみません。
答えていただけると嬉しいです。
また、問題集を何回回す、の定義ですが、間違えた問題だけを何回もやることでしょうか？それとも全問を何回もやることですか？もしくはそれ以外な感じなのでしょうか？
新しい参考書問題集を買うことに抵抗はありません。できれば薄くて、解説が詳しいもの、なぜそうなるのかが書いてあるものが好きです。
よろしくお願いします。
こゆきさんコメントありがとうございます。
基本的に私がいう周回はすべての問題を解くということです。
数学について。おそらく点数からして、まだあまり基本解法が定着していない状態だと思います。基礎問題精講なら一冊例題120問を3冊やれば、数学1a2b3と終わるのでおすすめです。私は基礎問を7周して基礎を固めました。できれば7周くらいしてほしいですが、時間もないでしょうから、まず4周して、その後は必要に応じて変化をつけてください。夏休み前には基礎問を終えて、一対一に入りましょう。かなり時間的に厳しいですが、やらないと合格は難しいです。そのまま一対一を周回し、冬休みからやさ理に進んで終わりです。
化学は共通テストで8割取れるまで、セミナーを周回してください。5,6周すれば十分だと思います。そのあと重問へ進めばギリ戦えます。
物理はエッセンスをネットや映像授業をつかいながら周回してください。数学に時間を取られるでしょうから、秋まで終わらせて、そのあと名門の森に進めばOKです。
英語はアップグレードは春休み中にさっさと周回して固めといてください。その後英頻かファイナル英文法の赤に進めば十分です。それよりリーディングが弱そうなので、レベル別やイチからなどをやってしっかり長文読解を鍛えないと二次では太刀打ちできねいと思います。
あと余談ですが、自分の弱点もわかっているようですし、こゆきさんなら自分で考えて勉強法を確立できると思います。正直その成績で医学部を目指すのなら一瞬たりとも無駄にできない状況です。私が提示する勉強法はあくまで私に最適であったものを一般化しただけで、ある一定以上の効果は得られても、こゆきさんにとって最大の効果になるとは限りません。自分にとって最適な方法を工夫していかなければこの先少々厳しいでしょうし、こゆきさんならそれができると思ってます。
dioさん返信ありがとうございます。
詳しく教えていただきありがとうございます。
数学の基礎精講ですが、”一冊例題120問を3冊やれば”とのことですが、例題のみやった方が効率が良いのでしょうか。
また、1対1ではなく標準問題精講で代用は可能でしょうか？（もっているというわけではなく、同じシリーズの方が解説などに一貫性があるのかな？と思ったためです）
英語のレベル別はどのレベルから取り組むべきですか？、一冊にかける時間や、一冊を何周するべきかも教えてほしいです。 レベル6までやろうと思っています。
英語のリスニングは何をすればよいでしょうか。リスニングは好きな方です。
化学のセミナー周回はいつまでに終わらせるとよいでしょうか？
お忙しいところ質問を重ねてしまってすみません。
よろしくお願いいたします。
こんにちは。
私は今年浪人を河合塾ですることになったものです。
数学が苦手であり計算ミスも多いため、春休みに克服しようと思うのですが、受かる数学か基礎問題精巧どちらをやれば良いと思いますか？(基礎問題精巧は以前3周ほどやりましたが完璧には出来ていないです)
七宮さんコメントありがとうございます。
既に3周ほどしているのであれば、基礎問題精講を極めるほうが成績は上がると思います。計算力は周回しているうちについてくると思います。頑張ってください。
前に高校受験について質問をさせていただいた中二のものです。
再びですが質問させていただいてもよろしいですか？
今から高校に向けての数学の先取りをしようと思うのですが、
基礎問題精構から始めても理解できるのでしょうか。
また、その後のルートも教えていただけると助かります。
ちなみに、中学分野はすべて理解できています。
fundaさんコメントありがとうございます。
基礎問題精講だけでは、まず無理だと思います。おそらく映像授業を参考にしつつ、基礎問を進めていく形になるかと。中2ということでしたら、東進の数学特待をとるか、スタディサプリが一番いいと思います。
基礎問題精講→一対一→プラチカややさ理、の順番で進めば問題ないと思います。
返信ありがとうございます。
その方法で頑張ってみます
重ねて質問よろしいですか？
数学特待の模試は全国という範囲でのでなければいけないのでしょうか？
(ただの公立中学生なので)
おそらくそうだったはずです。でも学校の成績が5ならもらえるので、そっちの方が簡単だと思います。
こんばんは、北大医志望の高2で来年受験生の男です。これまで全く勉強してこなかったせいで数学が壊滅的でどれくらい酷いかというと進研で60後半（点数）しか取れてない状況です…（ ｉ _ ｉ ）ニューアクションレジェンドという網羅系に手を付けたのですが来週の土曜日に共通テスト模試がある為、そこまでに間に合わせたいと思ってます。時間ならあります、1週間で基礎問例題を周回して付け焼き刃ですが対策にはなるでしょうか？また北大医でA判取るまで数学の点数を伸ばすにはこれからどの様な問題集ルートで行くべきですか？質問多いですが（焦ってます💦）答えて頂けると嬉しいです。
つ…詰みました… さんコメントありがとうございます。
1週間で基礎問例題を周回して付け焼き刃ですが対策にはなるでしょうか？
→どんな教科でも一週間後に結果を求めるのはさすがに無理があると思います。仮に一週間で基礎問を3周できるなら多少の成果は出ると思います。
北大医でA判取るまで数学の点数を伸ばすにはこれからどの様な問題集ルートで行くべきですか？
→基礎問題精講を使うなら、基礎問→一対一→やさ理で十分にA判定を取れると思います。多分これが一番効率的です。
地方国公立志望の高３です。共通テストはだめだめで、苦手な数学化学が足を引っ張りました。数学は本当に何も理解しておらず、数ⅠA49点、数II･B26点と悲惨な状態なのですが、二次試験に数学があります。
二次試験まで残り1ヶ月ほどしかないのですが、二次試験で高い点数を取らなくては行けません。基礎の基礎から徹底でき、過去問に繋げられるような参考書は何が良いでしょうか…。ネットで沢山調べてはいますが自分に合うレベルのものが分からず困っています…。よろしくお願いします。
高３さん
コメントありがとうございます。
あと１ヶ月ということを考慮して、過去問に繋げることができる参考書をあげるとすれば基礎問題精講しかないでしょう。本来ならば、過去問と同レベルの参考書を回してから過去問に入るのが理想ですが、今回は時間がないので過去問を解くための必要最低限の武器のみを基礎問で獲得して、あとはぶっつけ本番が最善だと思います。しっかり基礎問題精講で下地ができていれば、高得点は無理でしょうがある程度は解けると思います。
正直言わしてもらうと、その点数であと１ヶ月で国公立レベルにすることは不可能です。最後の悪あがきとして選択するなら、必要最低限の武器のみ調達することです。間違っても、難しい参考書には手を出さないようにしてください。おそらく分けわからずに無意味な１ヶ月を過ごすことになります。
数学は耐え、他の科目で数学の分も稼いであげてください。
返信ありがとうございます。
実は数学しか二次試験がないんです…。
でも、最後の悪あがき、頑張ります。本当にありがとうございます。
そうだったんですか！それは大変ですね。すべて出し切るつもりで頑張ってください。
現在自称進学校に通う理系の高校2年生で4月から高校3年生です。偏差値は進研模試で偏差値50～55くらいです。志望校は埼玉大学、東京理科大学です。現在基礎問題精構と合格る計算を平行してやっています。基礎問題精構1A2Bが終わったら基礎問題精構3と一対一1A2Bを平行して、やり終わったら一対一3をやろうと思います。6月から一対一をやろうと思います。基礎問題精構、一対一は4周します。終わりますでしょうか？今から埼玉大学、東京理科大学を目指すのは無謀でしょうか？だいたい１日何問何時間やるのが理想でしょうか？基礎問題精構をやったら進研模試で偏差値いくつぐらいになるでしょうか？質問多くてすみません。
にぶるすさんコメントありがとうございます。
終わりますでしょうか？今から埼玉大学、東京理科大学を目指すのは無謀でしょうか？
→全然終わると思いますし、順調に行けば余裕で目指せると思います。
だいたい１日何問何時間やるのが理想でしょうか？
→基礎問題精講なら10〜20問/dayくらいが理想的です。ただ他の教科の兼ね合いも見て一日の数学の勉強時間は1〜2時間程度に収めた方がいいと思います。（休日はもっとやっていい）
基礎問題精構をやったら進研模試で偏差値いくつぐらいになるでしょうか？
→正確にはわからないですが、基礎問題精講レベルの問題が全部解ければ少なくとも偏差値65はでると思います。場合によっては70も全然超えます。
受験となればみんな不安なので、質問が多くなるのも当然です。ぜひ頑張ってください。
返信ありがとうございます。計画が崩れないように頑張ります。
今年の新学期から新高校2年生になります。
大阪大学医学部志望の高1です。
高校1年生の時から鉄緑会に入りたかったのですが、入塾テストは全滅です。
母からは今年の3月のテストに受からなかったら諦めなさいと言われました。
でも、私は絶対に鉄緑会に入りたいんです。
コロナ自粛の時から青チャートをやっていましたが、全然終わらず、解法は解けば解くほど抜けていき、絶望していた時にこの記事を読ませていただきました。
当初は一対一の対応の記事を読ませていただいて、そのあとこの記事に出会いました。
ここで紹介されているように基礎問題精講を高速で回していけば、受かることは出来るでしょうか。それとも、一対一の対応をやった方がいいでしょうか。
(鉄緑会に入るには、駿台模試の数学の偏差値が60代後半でなければ厳しいそうです。)
ちなみに、10月の駿台模試の数学の偏差値は58.7でした。
長文乱文すみません。
ぜひお返事をいただけたら、と思います。
1Aさん
コメントありがとうございます。
高2の鉄の入塾テストだと、一対一対応の演習まで完璧にしてないと合格するのはキツイと思います。駿台模試で偏差値60弱あることと3月に入塾テストがあることを考慮すると、一対一を猛スピードで周回する方が鉄緑に入れる可能性は高いと思いますが、それでもは難しいとは思います。
私個人的には、鉄緑入塾にとらわれずに勉強した方が最終的には高い点数を取れるような気もしますが、ぜひ頑張ってください。一対一が完璧なら受かるはずです。
お返事ありがとうございます。
厳しいですよね…。
ひとまず、アドバイスくださった通り、一対一を完璧にしてみます。
また、6月のテストも受けれるよう親と交渉してみます。
もし、許可を貰えれば、基礎問題精講からの一対一をスピード重視で回していきます。
少し希望が持てました。
ありがとうございます！
現在高2の東大理一志望の者です。高一の頃から背伸びをして青チャート1A＆2Bを購入し、1Aの方は例題のみを2周＋α、2Bも例題のみを1周程回しています。共通テストレベルの模試(東進)では1A60点前後、2B50点前後とさすがに危機を感じています。
この記事を読んでこのまま青チャートを回していくべきか、いっその事思い切って基礎問題精講に変えて何周も回していくかで迷っています。お忙しい中だと思いますが、前者、後者どちらの方が良いか意見が欲しいです。
長文失礼致します。
topoさんコメントありがとうございます。
そこまでやっているなら青チャを周回しちゃえばいいと思います。あんまり基礎問題精講をやってる時間もないですし。なので、私としては前者ですね推しですね。
ご意見ありがとうございます。青チャートで粘ろうと思います！
札幌医科大学志望の高1です。今まで青チャートを解いてきたののですが、模試の成績が全く上がりません。そこで偏差値60くらいです。こんなのでも医学部目指せるでしょうか。これから数学2の勉強を始めるのですが基礎問題精巧→一対一で医学部目指せるでしょうか。これからの方針についてアドバイスお願いします。
Kさん コメントありがとうございます。
学年が上がるたびに模試の受験者は増えていくので、高1で偏差値60だと高3の終わりには偏差値50〜55程度になってしまうと思います。それではさすがに医学部は厳しいでしょう。ただあくまでも「現在のままなら」の話です。
基礎問題精講→一対一なら医学部は目指せるけど少し足りないです。合格者平均点には届かないと思います。これに、プラスして「やさしい理系数学」などの応用系問題集で演習を積めば医学部でも全然戦えます。
ただ、チャートで成績が上がっていないことからして「参考書が合っていない」か「参考書の使い方に問題がある」ので、そこはぜひ自分でもう一度見直してみてください。
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 【大学受験 数学】スタディサプリ数学の詳細と使い方を徹底解剖！ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
琉大医学部目指してる高2です。数IIの三角関数まで終わりました。どの参考書から始めてどのくらい目安でやっていけばいいですか？？
返信遅れてしまい、すいません。
同じコメント内に追加されると見逃すことが多くて。わざわざ、もう一度コメントしてもらいありがとうございます。
一応、↓の方に返信させていだだきました。
こんにちは
文系で金沢大志望の者です。
今は基礎問題精講を周回していますが、精講が仕上がってから演習の参考書か過去問に進むか迷っています。どちらにすべきかアドバイスをいただけると幸いです。
また、演習参考書にする場合は1体1や標問などで十分でしょうか。
TM さん
コメントありがとうございます。
確かに微妙なラインです。基礎問題精講だけでも戦い抜けるか、どうか。ひとまず基礎問題精講を仕上げた後に、過去問を１年分解いてみましょう。迷ったときは過去問で実力を計るのが一番です。解いてみて満足いく点数に近ければ、そのまま過去問を進めてください。形式に慣れれば点数は１割ほど上がります。
もし実力が不十分だと思ったら、「重要問題集（文系用）」をおすすめします。一対一や標問は十分すぎる感が否めないです。もちろん、使って損にはなりませんが、重要問題集でもA問題（とB問題）をメインに演習を重ねれば高得点も期待できます。
選択肢を増やしてしまって申し訳ないですが、お役に立てれば光栄です。
お返事ありがとうございました。
頑張ります。
琉球大学医学部を目指してます。
琉球大学は数Ⅲが多く出題される傾向にあります。ただ他の医学部と比べると難易度は低いです。どの参考書のレベルくらいまで仕上げると2次試験の数学で8割から9割取れるようになりますか？？
ででお さん
コメントありがとうございます。
琉球大医学部の過去問を拝見させていただきました。おそらく「一対一対応」が完璧になれば理論上８割９割は取れると思います。理論上というのは、本当に一対一レベルの解法を自在に操れたらということです。ただ全部を完全に吸収するのは難しいと思うので、解法の扱い方に慣れる意味でも「数学Ⅲスタンダード演習」や「やさしい理系数学」レベルまで仕上げておくと９割も安定して取れると思います。
もう一度言いますが、一対一まで仕上げれば本当は８割９割取れます。一対一までで、すべて終わらせる予定で参考書を完璧にしていくのが大切です。琉球医大なら満点も夢ではないので、ぜひ頑張ってください。
今高2です。数IIの三角関数まで終わりました。どの参考書から始めてどのくらいのスピードでやっていけばいいですか？？
私の使ったルートだと、「授業」⇒「基礎問題精講」⇒「一対一対応の演習」と進みました。「数Ⅱの三角関数まで終わった」というのが「授業」で理解したということでしたら、あと１ヶ月くらいで数学ⅡBの「授業」を見て理解し終えてください。（授業使わなくても理解できるなら、見なくてもいい）
そして数学ⅠAⅡBの「基礎問題精講」を６ヶ月間で。３ヶ月間を使って、数学Ⅲの「授業」と「基礎問題精講」を終わらせる。これで高２の２月末。平均１5問/日で進めれば終わります。残り１２ヶ月のうち、９ヶ月を使って「一対一対応の演習」を終わらせる。こちらも平均１２題/日でやれば、丁度いいくらいだと思います。余りの３ヶ月は予備兼「やさしい理系数学」です。
もし「数Ⅱの三角関数まで終わった」というのが「基礎問題精講」レベルは終わったという意味でも、基本は同じです。↑の予定の数学Ⅲのところから始めて、一対一対応は１２ヶ月くらい使って終わらせてください。
参考書は１周目は１０題/日くらいで、少しずつ一日に解く問題数を増やして平均が１５、１２なら大丈夫です。
ででおさんの現在位置が正確にはわからないので適切なアドバイスをできませんが、基本は「周回数×問題数÷日数」で計算するだけなので、↑のを適当にカスタマイズしてください。
長文になりましたが、お役に立てれば光栄です。
返事ありがとうございます😊
こんにちは、今日初めてサイトを見させていただきました
素晴らしいですね
質問失礼します
数1aのスタサプの講座を全て受け終わればすぐに基礎問に移る方が良いのでしょうか？
それとも、スタサプのテキストを完璧にしてからの方が良いのでしょうか？
匿名 さん
コメントありがとうございます。
私は、講座を受け終わったらすぐに基礎問に移る方でいいと思います。テキストの問題はたいてい基礎問にも載っているので、範囲被りますし。ただテキストの内容を今にも忘れそうで不安なら、一度テキストを解き直して復習してから基礎問に移るとスムーズに進むと思います。
褒めてもらえてうれしいですが、コメントは新しく作ってもらえると見つけやすくて助かります。
静岡大学工学部、明治大学理工学部志望の高三です。1A,ⅡBを基礎問題精講、数IIIは青チャートを使っています。数3はコロナの関係もあり、あまり授業が進んでいないためスタサプ＋青チャートで基礎固めをしようと思っています。数3も基礎問題精講の方がいいですか？あとⅡBとIIIなんですが、頻出問題のベクトル、数列、微積分、複素数平面は青チャートをやった方がいいですか？それとも、基礎問題精講を完璧にした方が良いですか？青チャートをやる場合はコンパス3までしかやらない予定です。どうしても青チャートの方が網羅性が高く心配になってしまいます。だったら青チャートをやれば良いのですが、時間がなくなる可能性を考えると基礎問題精講の方がいいのかなと思います。それらが終わったらcanpassと入試の核心をやる予定です。質問多くてすみません。回答よろしくお願いします。
こーへ さん
コメントありがとうございます。
まず私は基礎問題精講をやる方がいいと思います。実際、私も基礎問題精講Ⅲをやって基礎力を付けましたが申し分ない網羅性です。青チャートのコンパス３までと比較しても、まったく劣りません。青チャートはレベル幅が広いだけで、同レベル帯の問題種類なら基礎問題精講も同じくらいです。その上、あとで入試の核心に進むということでしたら尚更安心してください。
静岡大学工学部、明治大学理工学部は数学メインの学部ですが、基礎をしっかり抑えていれば十分に戦えます。また頻出分野も難しいわけではないので、まず基礎問題精講を完璧にしてから考えましょう。おそらくベクトル、数列、微積分、複素数平面が苦手単元というわけではないなら、それで十分なはずです。合格者最低点も取れるかもしれません。
最後に、campassと入試の核心はどちらかに絞って、その分基礎強化に時間も回した方がいいと思います。片方を極めれば合格者平均点くらいは取れると思うので、下手に先に進むより完璧な下地を作る方が安全策かと思います。
長文失礼しました。お役に立てれば光栄です。
返信ありがとうございます！！スタサプ＋基礎問題精講で数3の基礎固め頑張りたいと思います。引き続き1AⅡBの基礎問題精講を仕上げることを目標にやっていきたいと思います。演習問題集として入試の核心をやって過去問に入りたいと思います。これから数列、微積分、複素数平面、ベクトルを勉強していく中でもし苦手な単元が見つかった場合は青チャートを回すべきでしょうか？それとも、単元ごとに解説がされている面白いどわかるシリーズなどをやった方がいいのでしょうか？オススメなどあれば教えて頂きたいです。質問多くて申し訳ありません。
苦手にも種類があると思うので、しっかり分析してみてください。理解できなくて苦手なら、スタディサプリや面白いほどわかるシリーズなど解説重視でやり直すのがおすすめです。演習量が足りなくて分からないだけなら、基礎問題精講の該当単元（青チャートでも構いません）、Z会のSpeed攻略１０日間などの少ない問題数を何度も解き直すことで解消すると思います。
もちろん基礎問題精講ですべて習得するのが目標です。ぜひ頑張ってください。
ありがとうございます！精一杯頑張ります！！
dio様
丁寧な返信ありがとうございます。
繰り返しの質問申し訳ないのですが、一対一は標準問題精巧でも代用は残された時間を加味して考えても大丈夫ですか？《一応、標準問題精巧に関する記事は拝見しています≫
D4C さん
返信が遅れてしまい申し訳ございません。
標準問題精講で代用しても大丈夫だと思います。若干問題数は増えますが、たいした差にはならないので気に入った方を選んでください。
どっちを選んでも、一日にこなさなきゃいけない問題数は多いと思いますが、頑張って間に合わせてください。
応援してます。
こんにちは
高三の理系です。成績的に基礎問題を必ずやるべきの部類にいます。二つ質問したいことがあります。
一つ目は、一日何題のペースで進めればいいですか。
と、二つ目は志望は名大の理学部なんですけど、一冊ずつ進めているとおそらく間に合わないと思うのですが、三冊同時進行で進めていった場合のデメリットをお聞きしたいです。回答よろしくお願いします。
D4C さん
こんにちは。
コメントありがとうございます。
名大志望ということでしたら、一対一などもやると思うので１冊１ヶ月ペースだと理想的です。比較的時間もないので、「５周する」仮定でいきますと、一日２５問が目安ですね。周回数は、定着度と一日に解ける問題数を考慮して決めてください。
３冊同時進行のデメリットは１周する間隔（期間）が長くなることで、復習効率が落ちることです。名大合格のためには、どちらにせよ基礎問題精講レベルは完璧になる必要があります。１冊ずつ進めても結局のところ「解く総問題数」は変わらないし、復習間隔が狭くなればサクサク進むと思うので、私は１冊ずつ進める方がいいと思います。
dio様
丁寧な返信ありがとうございます。
繰り返しの質問申し訳ないのですが、一対一は標準問題精巧でも代用は残された時間を加味して考えても大丈夫ですか？《一応、標準問題精巧に関する記事は拝見しています≫
D4Cさん
返信が遅れてしまい、申し訳ございません。
ブログの構造を把握しきれてないもので、コメントを見逃してしまいました。
一対一を標問で代用するということですよね。大丈夫だと思います。多少問題数は増えますが、大差はないです。気に入った方を使ってみてください。
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 数学 例題だけはやめろ！１対１対応の演習のレベルと真の使い方 […]
Dio様、質問失礼します。
基礎問題精講後の進み方についてです。
私は新中3で、
基礎問題精講(スタサプと併用)、1対1対応、新スタ演を使い高校数学を独学することにしました。
数1Aの基礎問が今8周目で、次の参考書のことを考え始めたのですが、この後のルートは
数IIBの基礎問→数3基礎問→各学年の1対1→新スタ演
数IAの1対1→IIB基礎問→IIB 1対1→IIB基礎問→III基礎問→III１対1→新スタ演
どちらがいいでしょうか？
Dio様が実際どのような進め方をしたのか等も聞ける嬉しいです。
すいません、上のコメント無視して下さい。数III独学ルートのページに移動させていただきました。
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？ 数学 例題だけはやめろ！１対１対応の演習のレベルと真の使い方 […]
基礎問題精講の使い方について質問よろしいでしょうか？
・1A→2B→3 を1セットとして10周
・1Aを10周→2Bを10周→3を10周
どちらの順序でしょうか？
AAAさん
私のおすすめは後者です。
分かりにくい説明で申し訳ありません。訂正しておきます。
お返事ありがとうございます
どの程度やり込むべき参考書なのか迷っていたのでとても助かりました
基礎問題精講の使い方について質問です。
1周目から4周目は演習は飛ばして、例題だけひたすらやる
5周目から8周目は例題をやらずに演習だけひたすらやる
9周目、10周目は演習と例題を交互にやる
最後に10周しても分からない問題だけ解く
使い方の解釈はこれで合っていますか？
なたりーさん
そうです。そういうことです。
春休みを使って一気に進めてみてください。
説明が分かりにくくて、すいません。訂正しておきます。
ありがとうございます！
がんばります！！！
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ 【大学受験 数学】スタディサプリ数学の詳細と使い方を徹底解剖！ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ 【大学受験 数学】スタディサプリ数学の詳細と使い方を徹底解剖！ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ 数学 例題だけはやめろ！１対１対応の演習のレベルと真の使い方 […]
基礎門のチェバの定理間違ってません？
私の持っている「基礎問題精構ⅠA四訂増補版」の「基礎問５３ チェバの定理」を見る限りは、間違っているようには見えませんが。
私も気になるので、もう少し具体的に間違っている箇所を指摘して頂けるとありがたいです。
逆だと思うんです分母と分子
基礎問題精構ⅠA四訂増補版「５３チェバの定理のポイント」を例にとります。チェバの定理は分母を払った状態なら、
FB×DC×EA＝AF×BD×CE・・・➀
になります。
この後、右辺（AF×BD×CE）で➀の両辺を割ると基礎問５３のように右辺＝１です。左辺は「FB×DC×EA」が分子、「AF×BD×CE」が分母になりますよね。あとは、分母と分子を上下１セットで、３つの分数「FB/AF」×「DC/BD」×「EA/CE」）に分解すると基礎問５３のようになります。
しかし、左辺（FB×DC×EA）で➀の両辺を割ると基礎問５３のチェバの定理とは、分母分子が逆になって出てきます。
上手く説明できなかったですが、いかがでしょうか。
(A/B) × (C/D) × (E/F) = 1
ならば
(B/A) × (D/C) × (F/E) = 1
ですので、ぶっちゃけ分母・分子は全部逆でも
いっこうに差し支えないです。
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅系の基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学は薄い問題集こそ正義！薄いのに網羅性のある基礎問題精構とは？ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
大阪府立大学文系志望の高1です。
ベネッセ進研模試で総合の偏差値が４９～５２でGTZはB2からB1を行き来しています。数学と英語が足を引っ張っています．．．。
このままではどう考えても大阪府立大学に行ける成績ではありません。
でも、どうしても大阪府立大学に行きたいんです。同じ大学を志望していた友達はあきらめてしまいましたが、私はまだあきらめたくありません。
相談なんですけど、3月から数Ⅰ数Ⅱの基礎問題精構をはじめて、終わったら標準精構を完璧にしようと思っているのですが、一日何問を目標にしたら良いですか？また何月ごろに終わらせるのが良いですか？
hinataさん
コメントありがとうございます。
高2の前半6ヶ月で基礎問題精講が終わると理想的です。最悪8ヶ月かかっても問題ないでしょう。その後高3夏までの時間で標準問題精講をやれば余裕で間に合います。
そうなると基礎問題精講は一日10〜20問、周回数を重ねるたび一日に解く問題数を増やして進めていきましょう。標準問題精講は、基礎問題精講の順調さに左右されるので、そのときまた聞いてください。
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 薄い問題集こそ正義！チャートなんてやめて、基礎問題精構を使え！ […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャートはやめとけ！薄い問題集こそ正義だ。基礎問題精構 […]
[…] 数学 チャート以外で成績を上げる！基礎問題精構のレベルや次の本 […]
[…] 数学 チャート以外で成績を上げる！基礎問題精構のレベルや次の本 […]
[…] 数学の参考書 薄い本のすすめ チャート以外で成績を上げる！ […]
[…] 数学の参考書 薄い本のすすめ チャート以外で成績を上げる！ […]
[…] http://high-child.lolitapunk.jp/2018/07/29/%e6%95%b0%e5%ad%a6%e3%81%ae%e5%8f%82%e8%80%83%e6%9b%b8%e3… […]
[…] http://high-child.lolitapunk.jp/2018/07/29/%e6%95%b0%e5%ad%a6%e3%81%ae%e5%8f%82%e8%80%83%e6%9b%b8%e3… […]