数学的帰納法 不等式もこれで余裕！両辺の差を取る理由も解説！

今回は数学的帰納法の不等式編について説明していこうと思います。

数学的帰納法の不等式編はもちろん等式編よりレベルが上がります。（本当にちょっとだけですが）

なので、等式の数学的帰納法が出来ない人は不等式も難しいと思います。

しかし、

実は私は数学的帰納法の普通のバージョンの等式編はもう記事をを出しているのです。

パチパチパチパチ。

等式の説明と、なぜ数学的帰納法を使うと証明することが出来るのか、をこちらで書いているので、気になる人は見ていってください。

数学的帰納法 等式編 ドミノの例でわかりやすく解説！難しいなんて言わせない！

本題に戻しますが、数学的帰納法で証明する不等式ってだいたい、見ただけで「とりあえず、あとでやろう！」ってなるような問題が多いですよね。

数字や文字が複雑なんですよね。

しょうがないです。数学が好きな人は９９％意地悪ですから。

そんな不等式も基本的な流れを抑えれば解けるようになります。一部頭を使う部分もありますが、難しくないです。

是非、今回で不等式の流れを理解して、スラスラ解けるようになって帰ってください。

ということで、数学的帰納法の不等式編について始めていきましょう。

数学的帰納法の不等式　手順

まず手順ですが、等式とほぼ同じで

1. n=Aのとき成立すること
2. n=kのときに成立すると仮定すると、n=k+1でも成立すること

を確認したら終わりです。

『n=kのときに成立すると仮定する』というのは、『n=kを代入した式は正しいと思う』ということです。だから、n=kのときの式は成立していると思っていいんです。

n=k+1の証明では、基本的にn=kの式を使います。

あれ？と思っていた人いましたか。

手順のところで、

１ではn=Aとなっていますね（Aはなんでもいいです）。不等式ではよく、『ｎ≧Aのときこの式を証明しなさい』みたいな問題が出ます。

例えばA=4だったとしましょう。このときに証明でn=1から始めても意味ないです。

証明しないといけないのは「４以上の数で成立するか」なので、n=1で成り立つかはどうでもいいのです。

注意ポイントとして証明のスタートはどこか、を意識しましょう。

数学的帰納法の不等式で両辺の差を取る理由

ここは、既に両辺の差をとる証明方法を見たことがあるという人向けなので、「そんなのやったことない」という人は飛ばしてください。

よく、数学的帰納法の不等式の解説を読んでいると「両辺の差」がいきなり出てきて、勝手に０より大きいとか言って

気づいたら証明終了。

たぶん、こんな感じですよね(笑)。

では、なぜ両辺の差が０より大きいと証明できるのか。基本的に問題では

A＞Bを証明するときに、A－Bを計算して０より大きいと言っているはずです。

A－B＞０（AーBが０より大きい）のときから逆に考えていきましょう。

A－B＞０

A－B+B＞０+B

A＞B

おお。AーB＞０ は A＞B と同じ意味だったのか！

でも、なぜわざわざ差を取るのか。

それは差を取ったA－Bのほうが考えやすいからです。A－Bを計算してCとなったとしましょう。C＞０の証明は、Cの最小値が０より大きければいいのです。

二次関数（範囲ナシ）なら

（https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1471787494より）

この図より頂点が最小値です。この最小値が０より大きいので、すべての値は０より大きいですよね。

一番小さい値が０より大きいんだから、他の値も０より大きいんです。

差を取らないと、AとBの２つのグラフを考えて大小関係を比べることになるので面倒です。

両辺の差を取る理由をまとめると、

• AーB＞０はA＞Bと同じ意味
• AーB＞０は最小値を考えるだけで良い
• 逆にA＞BはAとBの２つのグラフを考えないといけない

ということで両辺の差をとってまとめた方がメリットが多いのです。（メリット少なかったらやらないか(笑)。）

では、本題の数学的帰納法の不等式の説明に入ります。

てか、「数学的帰納法の不等式」って長いな。「数的不」みたいな略称がほしい(笑)。

数学的帰納法　不等式編　例題

（数学的帰納法の式じゃないけど）

まあ、日本語で説明ばっかりしてても眠くなってくると思うので、問題を見て説明していきます。

例題

ｎ≧５を満たす自然数ｎに対して、次の不等式が成立することを証明しなさい。

n²＜２ⁿ・・・・・・・・♡

＜方針＞

まず、n=5のときに成立することを確かめましょう。そして、n=kのとき成立すると仮定して、n=k+1のとき成立することを証明します。

＜ポイント＞

ここ重要なので、絶対読んでください！

• スタートはn=5。
• n=kの式は片側（右辺でも左辺でも）をn=k+1の式に変える。
• n=k+1の証明では差を取って考える。

＜解答＞

(ⅰ)n=5のとき

（♡の左辺）＝5²=25、

（♡の右辺）＝２⁵=32

よって、n=5のとき♡は成立する。

このとき、

（ⅰ）n=5のとき

（左辺）＜（右辺）

とか、

２５＜３２

みたいに勝手に自分で計算してしまうのは減点対象です。ここでは、左辺が右辺より小さいことを証明したいので、計算結果だけを書くのはNGです。

あと、n=1のときを書いても当然ダメです。

スタートはn=5なんで。

続き行きます。

(ⅱ)n=kのとき

ｋ²＜２^ｋ・・・☆

が成立すると仮定する。☆の両辺に２をかけると

2ｋ²＜２^ｋ+1となる。

仮定するところまでは、もとの式にkを代入しただけです。問題は

なぜ２をかける！！！！！！

思いますよね。

目的は（右辺）をn=k+1のときの式にしたい、そして２^ｋ+1＝２×２^ｋなので２をかけてn=k+1のときの形に持っていくわけです。

そうすると左辺は変化してしまいますが、

２ｋ²＜２^ｋ+1

になるわけです。あとは、n=k+1のときの左辺である(ｋ+1)²を使って、

(ｋ+1)²＜2ｋ²

を証明すれば、２ｋ²＜２^ｋ+1と合わせて、

(ｋ+1)²＜2ｋ²＜２^ｋ+1

(ｋ+1)²＜２^ｋ+1

になるわけです。ちなみに、A＜B＜CときはAよりBのほうが大きくて、BよりCのほうが大きいので、A＜Cですよね。

次に(ｋ+1)²と2ｋ²の大小関係を比較する。

ｋ≧５のとき

(ｋ+1)²ー2ｋ²＝ーｋ²+2ｋ+1

=ー(ｋー1)²+2＜０

軸がx=1で上に凸のグラフです。頂点は（１,２）です。下の図参照。

この場合は０より小さいことを証明するので、ｋ≧５のときに式が負になることを確認します。

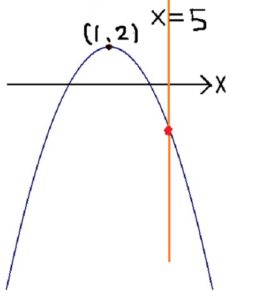
（汚くてすいません。実際はxをkに置き換えて考えてください。）

このとき、５以上ではグラフは負ですよね。だから、５≦kのときに

ー(ｋー1)²+2＜０が成り立つわけです。（この式と☝のグラフは同じ）

そして、(ｋ+1)²ー2ｋ²=ー(ｋー1)²+2＜０なので、A－B＜０ですよね。Aは(ｋ+1)²、Bは2ｋ²です。

A－B＜０なのでA＜Bです。不等号の向きは変わらず、移行するだけです。注意しましょう。

よって、

(ｋ+1)²＜2ｋ²＜２ ^ｋ+1

(ｋ+1)²＜２ ^ｋ+1

したがって、n=k+1のときも成立する。(ⅰ)、(ⅱ)より５以上のすべての自然数について♡は成立する。

どうでしたか。

一応、もう一度まとめておきます。

(ⅰ)n=5のとき

（♡の左辺）＝5²=25、

（♡の右辺）＝２⁵=32

よって、n=5のとき♡は成立する。

(ⅱ)n=kのとき

ｋ²＜２^ｋ・・・・・・☆

が成立すると仮定する。☆の両辺に２をかけると

2ｋ²＜２^ｋ+1となる。

次に(ｋ+1)²と2ｋ²の大小関係を比較する。

ｋ≧５のとき

(ｋ+1)²ー2ｋ²＝ーｋ²+2ｋ+1

=ー(ｋー1)²+2＜０

よって、

(ｋ+1)²＜2ｋ²＜２ ^ｋ+1

(ｋ+1)²＜２ ^ｋ+1

したがって、n=k+1のときも成立する。(ⅰ)、(ⅱ)より５以上のすべての自然数について♡は成立する。

やっぱり、大小関係を比較するあたりが難しいですよね。でも、それ以外はどの問題も数字が変わるだけです。

大小関係を比較するときは、

片側（右辺でも左辺でも）を強引にn=k+1の形にする。そして、もう一方（n=k+1に合わせてない方）を使って比較する。

慣れてくれば、簡単です。片側をn=k+1に変形して、計算するだけ。ほとんど機械的に出来ます。

あと、不等式の証明ではよく、もとの不等式とは別の不等式を証明することになります。

別の不等式が出てくることは普通のことなので、安心して先に進んでください。

では、類題いきますか。

数学的帰納法　不等式編　類題

（数学的帰納法の式じゃないけど(笑)。）

ぜひ、自分で紙に書いて解いてみて下さい。もし、電車の中などで書けないときは、流れだけでも考えてから解答を見てください。

類題

３≦ｎを満たす自然数ｎに対して、次の不等式が成立することを証明せよ。

２ⁿ＞3nー2・・・・・・♡

＜方針＞

いつもと同じように、まずn=3のときを証明します。n=kのとき成立すると仮定して、n=k+1が成り立つことを証明します。

そのとき、n=kの片側をn=k+1に変形してから頑張ってください。

＜ポイント＞

ここも重要です。

• スタートはn=３。
• n=kの式は片側（右辺でも左辺でも）をn=k+1の式に変える。
• n=k+1の証明では差を取って考える。

＜解答＞

(ⅰ)n=３のとき

（♡の左辺）＝２³＝８、

（♡の右辺）＝３×３ー２＝７

よって、n=３のとき♡は成立する。

(ⅱ)n=kのとき

２ ^ｋ＞3ｋー2・・・☆

が成立すると仮定する。☆の両辺に２をかけると

２^ｋ+1＞２(3kー2)となる。

次に３(k+1)ー2と2(3kー2)の大小関係を比較する。

3(k+1)ー2はもとの式の右辺にn=k+1を代入したものです。

ｋ≧3のとき

3(k+1)ー２ー2(3kー2)=ー3k+5＜０

よって、

２^ｋ+1＞2(3kー2)＞３(k+1)ー2

２^ｋ+1＞３(k+1)ー2

したがって、n=k+1のときも成立する。(ⅰ)、(ⅱ)より３以上のすべての自然数について♡は成立する。

どうでしたか。出来ましたか。

相変わらず比較するところが一番難しいですが、それでもたいしたことないですよね。

今回２つの問題で説明しました。

是非、この問題を何度か解いて、流れを自分のものにしてください。

まとめ

自分で数学的帰納法を解けるようになるためには、何度か解答を書く練習が必要です。

今日説明した２つの問題で練習していただけると私もうれしいです。（一応、頑張って書いているので）

今日の名言

明日はなんとかなると思う馬鹿者。今日でさえ遅すぎるのだ。賢者はもう昨日済ましている。

（チャールズ・クーリー）

ってことなので、今日から、いや今から数学的帰納法の練習始めてみましょう。

 

 

【学生の不思議①】数学：なぜ２や３の０乗は１になるの？０の０乗は？