今回は「学生の不思議」シリーズの第2弾で、「なぜ１＝0.9999…が正しいのか」という記事になります。
イェーイ
空前絶後の超絶孤高の「学生の不思議」！
ということでね。今はもうTV出演の少なくなったサンシャイン池崎さんのネタを借りました(笑)。
話が脱線しそうなので元に戻すと、
感覚的には違和感を感じますが、数学的には「1=0.9999…」は正しいんです。厳密なことは大学数学でやるらしいです。
高校生の中には知っている人も多いと思います。高校数学ⅠAの循環小数のところで習いますよね。
では、その「１＝0.9999…」がなぜ正しいのかを説明していこうと思います。
厳密な証明でないのもあるけど、みんな気にしないよね！
目次
１＝0.9999…が正しいことの証明
①分数を使った証明
まずは分数を使った証明。おそらく、これが一番有名だと思います。
１＝1/3×3
次に
1/3 =１÷３=0.33333…
を代入します。
１＝0.333…× 3 = 0.999…
というわけです。
あっさりしていますね。使った式と計算方法は小学生レベルですが、１＝0.999…が証明できました。
実は、この証明は厳密なものではなく一部強引に話を進めました。
＜問題点＞
まず、問題点として
1/3=0.3333… の計算がまだ終わっていない。
が挙げられます。これにより、
0.3333…の計算が完了していないのに、「1/3」と「＝」で結んでいいのか。本当に「＝」なのかということ。
そんな疑惑が残ったまま、計算を進めていくのは雑じゃない？
ということです。でも、感覚的にはこれでOKかな。
②文字で置いて証明
これが高校数学ⅠAの循環小数のところで習うやつ。
x=0.9999… とおく。
両辺を１０倍して 10x=9.9999…
これらを連立して
10x=9.999…
－) x=0.999…
9x=9
∴ x＝0.999…＝１
こちらも結構「あっさり」していますね。そろそろ「こってり」も食べたい頃です。ちなみに今日のお昼ご飯は豚骨ラーメン。
＜問題点＞
人間の手で計算するときも、一番右端の桁から計算を始めますよね。そのときに、一番右の端がない。
どうやるの？
つまり
0.999…と9.999… という桁が無限に続く数に対して引き算は出来るのかということです。
桁が有限の数（1.25や7.28など）で成立していた計算法則が、無限の場合も使えるかは微妙。確証が持てません。
ということです。
毎回、数が無限に続いてしまうがゆえに起こる問題です。
③割り算を利用する
こちらはあまり見かけない方法。
パソコンの分数は出来るだけ使いたくないので、「÷」の記号を多用します。すいません。
x=0.999…、y=1とおく。
（0.999… + 1)÷２＝0.999…
つまり、
(x+y)÷２＝x
両辺に２を掛けて、
x+y＝2x
y＝x
∴ 1＝0.999…
またまた、「あっさり」。だから、そろそろ「こってり」持って来いよ。
ちなみに、今日のお昼の豚骨ラーメンには「アボカド」と「チャーシュー」が入ってました。意外とアボカドが合う。
＜問題点＞
(0.999… + 1)÷2=0.999…
と
ｘ＝0.999…
の…は等しいのか。
こちらも、数が無限に続くため計算が完了しない。だから、完璧に一致している確証が得られない。
④引き算を使う
これが最短。（たぶん）
いきなり
１－ 0.999…＝ 0.000…
これにより、「１」と「0.999…」の差がない。
∴ 1 = 0.999…
すごい速い。一瞬で証明が終わりましたね。
ラーメンもこれくらいの時間で出来てくれれば、いいんですけどね。
＜問題点＞
これは、「１」と「0.999…」の差が見つからなかったので、同じと
みなしただけ。
同じかはハッキリしてないわけです。これは、無限によるものです。
しかし、「ε-δ論法」を使うと無限に続くことをきっちり説明できます。私も超表面的な部分しか知らないので、気になる方は↓
https://ja.wikipedia.org/wiki/イプシロン-デルタ論法
ここで勉強してください。
⑤無限等比級数を使おう！
これは数学Ⅲの話なので、知らない人も多いと思います。
等比数列は知っている人が多いと思うのでそこから話始めます。等比数列を知らない人は、適当に流してください。
まず0.999…を等比数列へ
0.9999… = 0.9+0.09+0.009+…
となります。この右辺は初項が0.9で、公比が0.1の等比数列です。書き換えると、
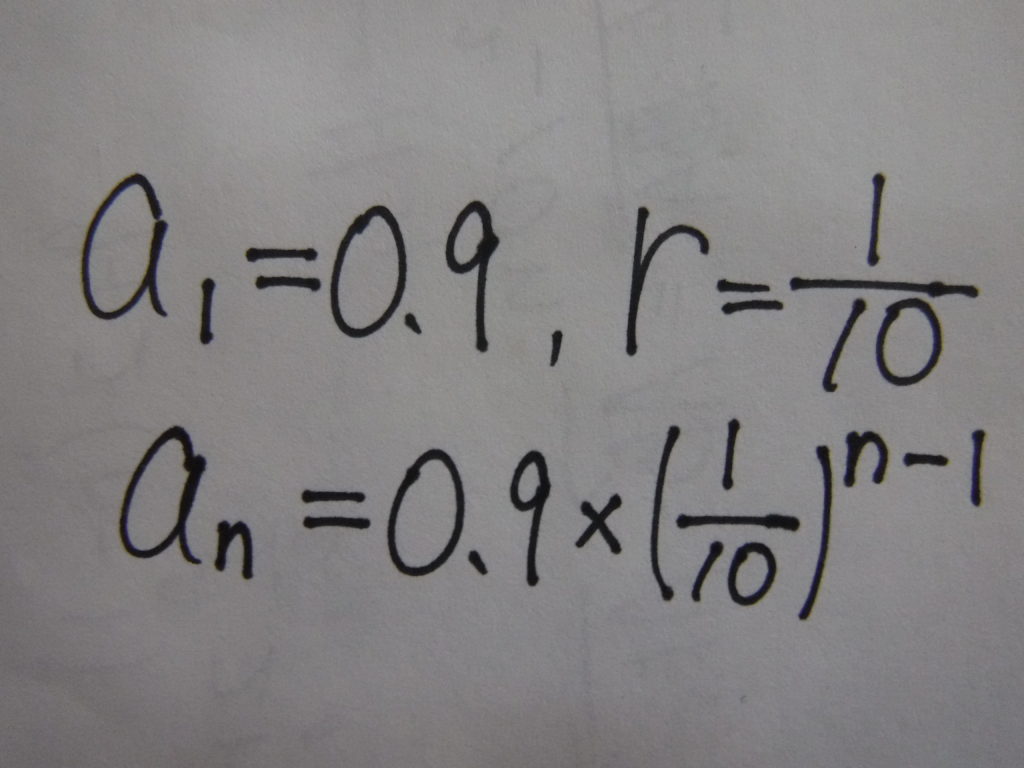
こうなります。
この等比数列の和を考えていきます。
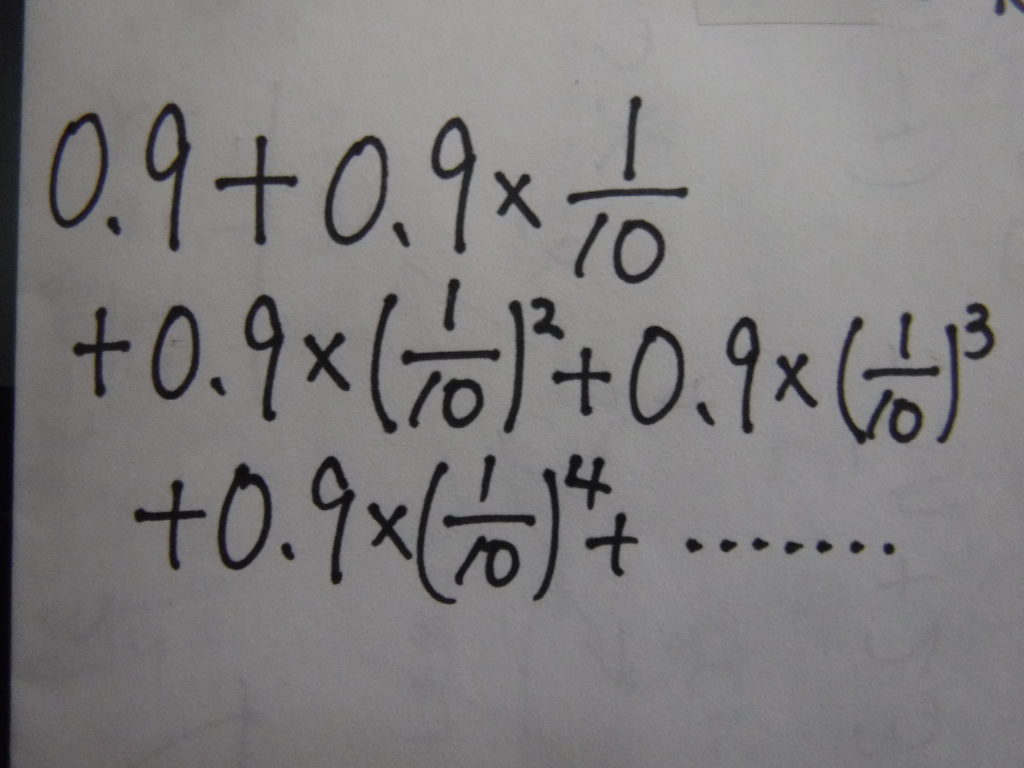
これってつまり、
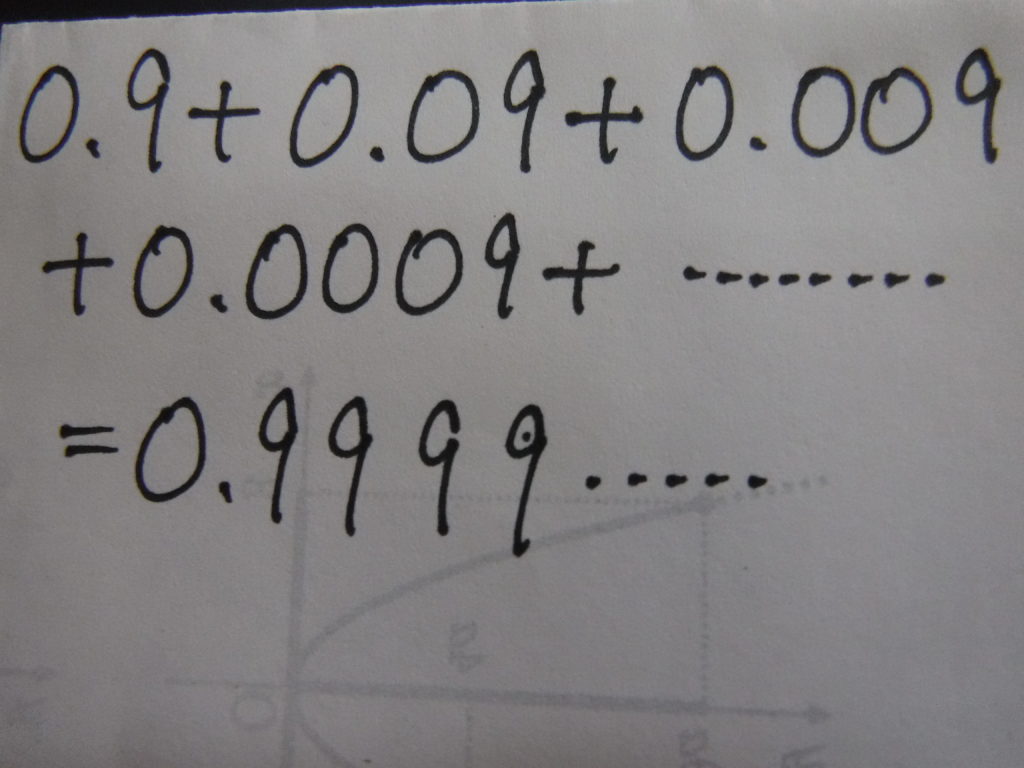
なわけです。
次に無限を考えていく
普通、等比数列だと １～ｎ までしか考えませんよね。しかし、今回は
0.999… と「９」が無限に続くわけです。
ということで、等比数列も無限まで考えていこう！となります(笑)。
ｎを無限大まで大きくすることを、「lim」の記号を使って
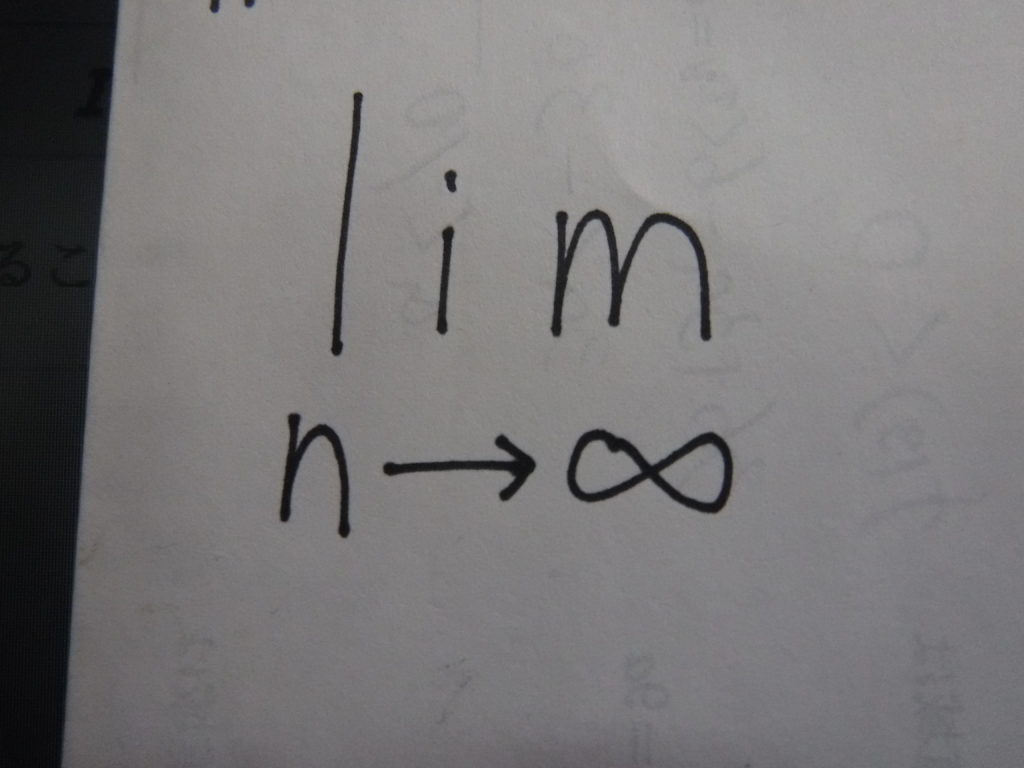
と表し、数列の和に対して「lim」をつけたときの数式の意味は
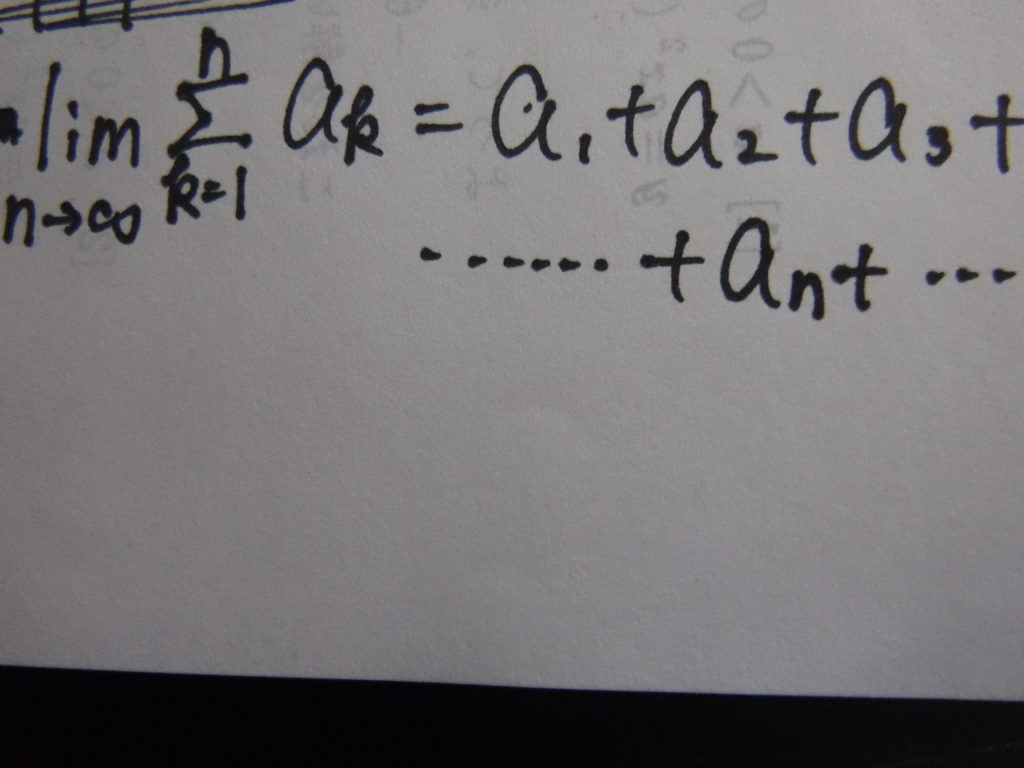
になります。
ついに無限等比級数
今まで考えてきたことより、
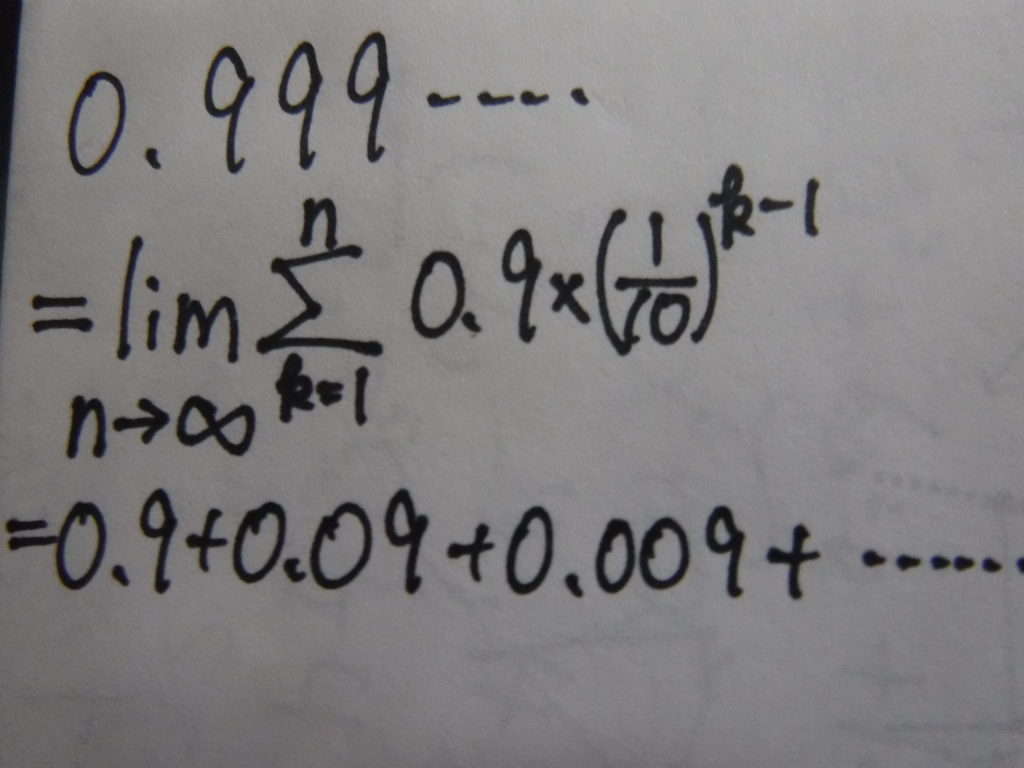
で、等比数列の和の公式は
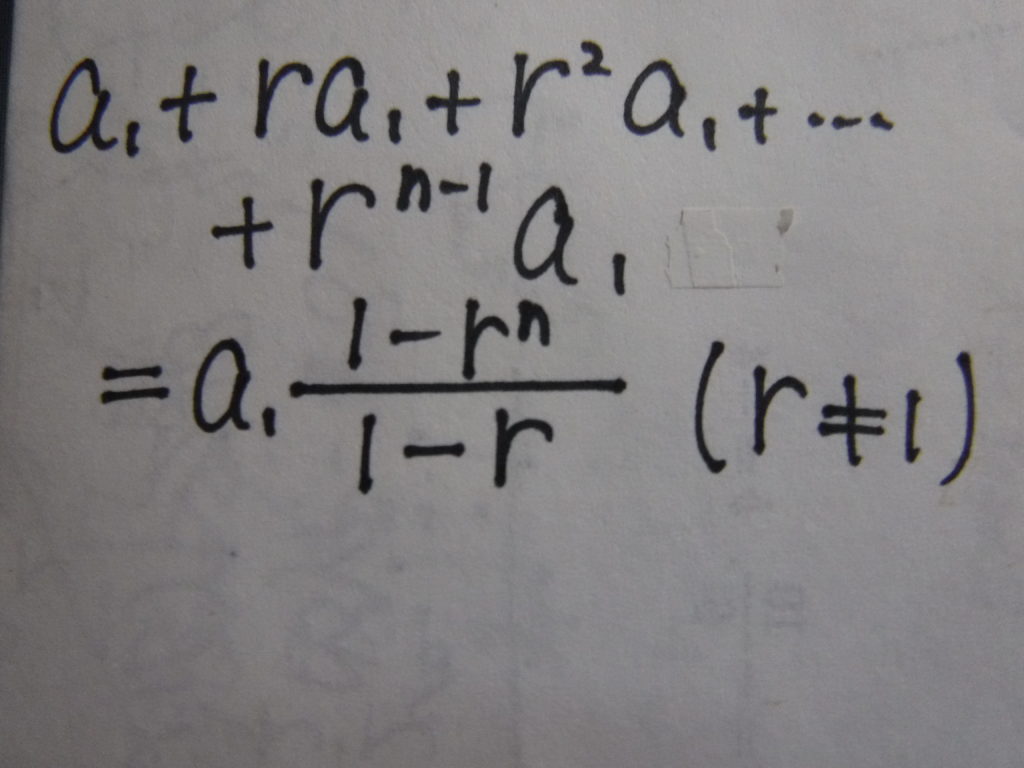
だから、これをｎ―→∞にして計算する。
－1＜ r=0.1 ＜１なので
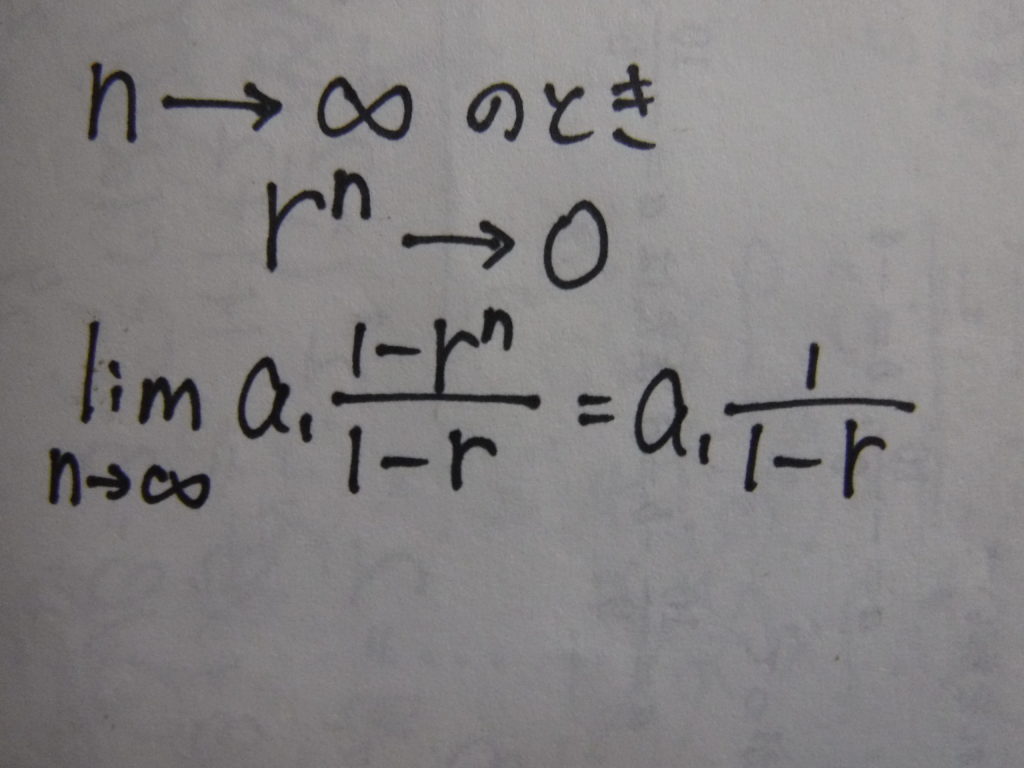
これにa=0.9、r=0.1を代入して
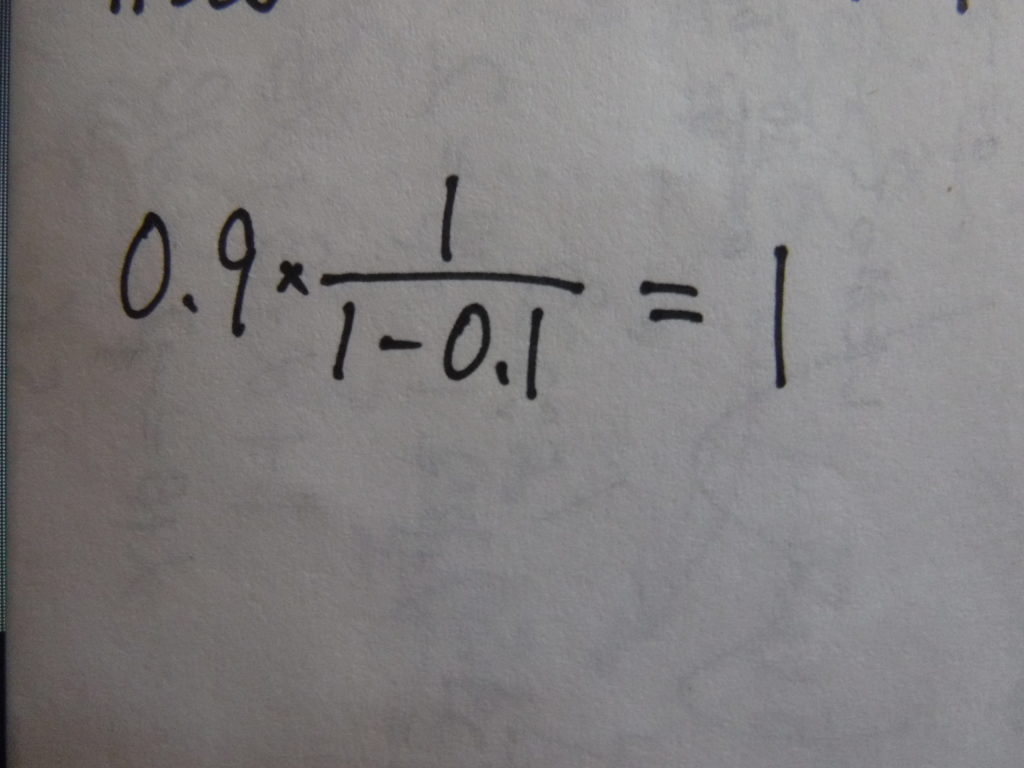
綺麗にまとまっているやつは
というわけで、
1=0.999…
と言いたいところですが、
＜問題点＞
「lim」記号でｎ―→∞にするというのは
ｎを∞に飛ばしたときに、その値が限りなく～～に近づく。つまり、その値にはなるわけではない。
限りなく近づく
という言い方です。
実際に、その値を取るかは別問題です。
コラム：計算機（電卓）を使うと
計算機（電卓）に
「１÷３×３」
と
「１÷３ → ×３」
の２通りで計算させてみてください。
私のアンドロイドの場合、「1÷３×３」にすると答えは１って出ます。
しかし、「１÷３」を押して、「＝」ボタンで計算させた後に「×３」を押すと答えは0.999…って出ます。
天下の計算機（電卓）でも、答えが２通り出てしまう。
この「１＝0.9999…」問題。
まとめ
結論
「1=0.9999…」は数学的には正しい。
しかし、それには大学数学を使わないと厳密な証明はできない。
この「中高数学の不思議」シリーズは中学、高校数学での不思議を解明していきたいので、大学数学は使いません。
（実際は私が使えないだけ(笑)。すいません）
是非、今後の「中高数学の不思議」シリーズを見て言ってください。ちなみに、第一弾は↓
[…] 【学生の不思議②】数学：なぜ1=0.9999…が正しい？誰でもわかる証明５選 […]
[…] 【学生の不思議②】数学：なぜ1=0.9999…が正しい？誰でもわかる証明５選 […]