超コスパ◎！『理系入試数学の核心(標準編)』のレベル＆使い方

　

最近スマホ版のカルチョびっとにハマっていて、これまた面白い。

育成ゲーム好きな人にはおすすめです。

　

今回は、

「理系入試数学の核心(標準編)」

を紹介します。

　

昔は自分が使う参考書しか基本的にみている時間がなかったんですけど、最近は使ってない参考書も見れるようになってきたので、

• 理系入試数学の核心
• 厳選！大学入試数学問題集

あたりを紹介したいと思います。

あと確認のために言っておくと、

紹介する参考書は”おすすめ参考書”とは限らないです。参考書の特徴をまとめるために作った記事もあるので、使用するか否かは自分でしっかり考えてください。

まあ基本的におすすめできるクオリティのあるもの、私の名前で紹介しても不名誉にならないものを選んでいるので、いい参考書ばかりなのは確かですが。

　

　

　

理系入試数学の核心(標準編)
基本事項

理系入試数学の核心(標準編)
対象者

• 国公立大学志望
• 典型問題は完成
• 時間的余裕はあまりない

　

国公立大学や早慶の下位学部を受験する人に非常におすすめ。

MARCHの上位でも数学で稼ぎたいなら使ってどうぞくらいの難易度になっています。旧七帝大でも最低限レベルは稼げるか稼げないかくらい。

主に下位〜中堅国公立志望の人におすすめです。

　

典型問題は完成している人が対象です。

大学受験数学を解く上で最低限必要なインプットはすでに終了している、典型問題の解法は頭に入っている、という人が使う参考書。

このくらいの問題なら、スッと第一方針は立ってほしい。

「sinとcosの対称式だ。ってことは、sin+cos=tとおけば、sin×cosもtで表せるから…」くらいは気付いてほしいです。

しっかり基礎的な典型問題を学習していれば、容易に気づける問題です。

これら典型問題を様々な視点からアウトプットできるのが「理系数学の核心(標準編)」になります。

　

　

そして、

時間的余裕がそこまでない人におすすめ。

通常数学1A,2B,3Cの全範囲で入試標準レベルを勉強しようと思ったら、1日にとる勉強量にもよりますが１年前後かかります。

ただそんな時間は残されていない。
短い時間で最大効率で勉強しないと間に合わない。

という人におすすめ。

本当に頻出な良問のみを集めているので、コスパは最強です。

　

　

　

理系入試数学の核心(標準編)
レベル

前提レベル：共通テスト８〜９割
到達レベル：地方国公立合格

　

＜前提レベル＞

前提レベルとして、共通テストで８割は取れるレベルでいたい。

他のwebサイトとかだと「共通テスト７割でOK」とか言っていますが、基本的に１冊目に選んだ参考書を完璧にすれば共テ８割は超えるはずです。

まだ７割なら、今やっている参考書を完璧にしてから進んできてください。

基礎問題精講や黄チャートのみだと少ししんどい。多分初見の正答率は3割程度になると思います。青チャートや一対一までやっていると初見正答率は5,6割程度で演習しやすいでしょう。

分野ごとの重要事項まとめなどはショボいので、先ほど紹介した通り、以下のような問題は即方針が立つレベルでないと厳しいです。

この問題が初見でできるレベルなら結構スムーズにいくと思います。

　

　

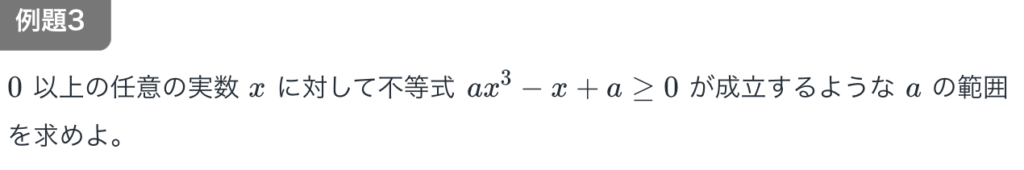
＜到達レベル＞

到達レベルとしては地方国公立大学の合格レベルになると思ってください。

一橋や東工大、旧七帝大や早慶などを目指す人には物足りない。MARCHなら点数が稼げるレベルになるでしょう。

　

感覚としては、

新数学スタンダード演習をまんま圧縮したような参考書です。

東京出版でいうA問題１割、B問題6~7割、C問題2~3割みたいな問題収録になっていると思っていただければ結構です。

一対一のアウトプット用教材、プラチカのやや易版、くらいのレベル帯です。

　

　

　

理系入試数学の核心(標準編)
内容

「１セット３題」で50セットあるので、合計150題。それぞれに小問もついていて、１セットで実際の入試形式みたいな感じです。

問題はそれぞれ３段階にレベルわけされていて、「★」「★★」「★★★」の順に難しくなります。

	問題数
★	28題
★★	82題
★★★	40題
合計	150題

★は入試基礎レベル。東京出版A~Bレベル。
★★は入試標準レベル。Bレベル。
★★★は入試標準〜応用レベル。B~Cレベル

　

その後セットごとに解説がなされます。

解説は

• 「考え方」
• 「Process」
• 「解答」
• 「核心はココ!」

の４パートから構成されます。

　

「考え方」は、設問を解く上での注目ポイント、一番重要な考え方を解説してくれています。

「Process」は解答の流れを抽象化してフローチャートで視覚的にわかりやすく解説したものです。非常に復習の際に有効になります。

「解答」は記述答案の模範解答。自分の記述チェックにもなります。

「核心はココ!」は他の問題にも応用できる「一般化された解法の法則」を簡潔にまとめてくれています。

「百聞は一見に如かず。」なので、とりあえず見てみてください。

　

　

また理系入試において頻出な、

• 場合の数・確率
• 数列
• ベクトル
• 微分積分

は他の分野よりも少し多く収録されています。

　

　

　

理系入試数学の核心(標準編)
特徴

①圧倒的少数精鋭

理系入試数学の核心(標準編)の一番の特徴は、

収録問題の少数精鋭さ

　

他の入試本番レベルの演習書（新スタ演やプラチカなどなど）と比較すると一目瞭然なんですけど、理系入試数学の核心(標準編)は、

圧倒的に問題数が少ない

参考書	総問題数 (1A2B3C)
理系入試数学の核心(標準編)	150題
文系プラチカ1A2B ＋理系プラチカ3C	149+76題
新数学スタンダード演習 (4月号＋5月号)	約300+約150題
やさしい理系数学	50+150題 (例題＋演習問題)

　

収録問題数が少ないので、周回時間も短くて済むし、サクサク進めることができます。

しかも、

中でも学習効果の高い、上級の頻出・典型問題を厳選しているので、非常に効率よく演習を積むことができます。

もちろん、

演習量そのものの低下によるアウトプットの練習不足、カバー範囲の欠損はあるんですけど、同じ問題数解くなら「理系入試数学の核心(標準編)」の学習効果がNo.1です。

個人的には、

十分時間がある
→プラチカ
時間があまりない
→入試数学の核心(標準編)

をおすすめしたい。

　

　

　

②「核心はココ!」が有能すぎ

理系入試数学の核心(標準編)の解説は非常に詳しいので、それだけでも十分推せるんですが、それ以上に素晴らしいのが

「核心はココ!」

「〇〇のパターンは△△で解けばいい」というふうにパターン化してくれています。

　

ありがたすぎる。

基礎〜標準的な内容なら、一対一などでもうパターン化していると思います。ただ、そこから一歩踏み込んで解法を超一般化してくれています。

エグい。

解法の一般化というのは非常に大事で、初見の問題への対応力に影響してきます。

理系入試数学の核心なら初見の問題への対応力がメキメキつきますから、少ない問題数でもしっかり実力を養成できると思います。

　

解答も詳しいし、Processではフローチャート化してくれるし、核心はココ!で要点は一発でわかるし、実質カリスマ講師の授業を受けているようなもの。

予備校の完璧な板書みたいな感じ。

　

　

　

理系入試数学の核心(標準編)
使い方

１日数学に1.5時間程度かけれる想定で考えます。

じっくりやるなら全問3周直し3周で7.5ヶ月、サクサクっとやるなら全問2周直し2周で5ヶ月ほどになるでしょう。（正答率は50%想定）

目安期間：5〜8ヶ月
ペース　：3題/日
周回数　：「3周＋直し3周」or「2周＋直し2周」

　

＜やり方＞

1. 3題を解く
   (40~80分)
2. 採点&解説熟読
   (30分)
3. Process&核心はココ!の復習
   (5分)

※セットで解く
※解けない問題も粘る
※Process&核心はココ!は理解が大事

　

1題1題とくでも、1セットで時間を測って本番形式で解くでもいいです。

1題ずつ解く場合は20分、セットで解く場合は3題合計で60分を目安に解きましょう。解けない場合も、この時間までは試行錯誤して粘ることで力がつきます。

解説を熟読して理解したら、

1日の復習として、「Process」と「核心はココ!」をもう一度おさらいすると非常に効果があると思います。

　

理系入試数学の核心(標準編)
接続

理系入試数学の核心(標準編)の前後にやるべき参考書を紹介します。

　

理系入試数学の核心(標準編)
前の参考書

• 一対一対応の演習
• 標準問題精講
• 青赤チャート
• （基礎問題精講）
• （黄チャート）

　

基本的には、一対一や標準問題精講の後にやるのがおすすめ。赤青チャートでも可という感じです。

理系入試数学の核心(標準編)を典型問題のインプットとして使う場合に限り（何周もする）、基礎問題精講や黄チャートの後に使ってもいけなくはないです。

でも、

典型問題のインプットをしっかりするなら、問題数多いに越したことはないので、時間が許すのであれば一対一等を使った方がいいとは思います。　

『1対1対応の演習』例題だけはOUT！理Ⅲに受かった使い方とは!?

【数学】標準問題精構の例題だけは危険！最高の使い方とレベル。

　

　

理系入試数学の核心(標準編)
後の参考書

• 過去問
• プラチカ
• やさしい理系数学
• 新数学スタンダード演習
• ハイレベル理系数学
• 理系入試数学の核心(難関大編)
• 上級問題精講
• 新数学演習

などなど。
（ちなみに理系入試数学の核心(難関大編)はゴリむずいです。）

　

一応、

想定使用方法としては過去問の直前です。

この後過去問に入って、演習と研究をして、受験するという時期に使うのが適切かと思います。

もし過去問との間に時間が余るようなら、最初から問題数の多いプラチカなどを使用した方が効果的に成績は上がるでしょう。

　

後半４つに進むなら、少し覚悟しないといけません。

理系入試数学の核心(標準編)はどうしても問題数が少ないので、その演習量で凸ると普通に初見正答率が終わります。

だから、

前半３つの同レベル帯の参考書で演習量を積んだ方がいいかなと思います。

【数学】一対一の次は文系の良問プラチカで決まり！王道は裏切らない！

東大でも通用する！「新数学スタンダード演習」のレベルと真の使い方！

　

　

まとめ

現役時代は使いませんでしたが、「理系入試数学の核心(標準編)」は非常に良書です。

ぜひ使ってみてください。

　

　　

　

【大学受験】俺のガチおすすめ！数学の参考書ルートを紹介！