【数学】『入門問題精講』がほぼ神講義のまとめノートな件。

　

最近ですね、仲の良い東大生と遊んでいたらですね、N君とT君がお互いディスりあいを始めまして。まあ、それはいつものことなんですけど。

どっちがブスか、という言い争いをしていたら、

ドンドンエスカレートしてそのままガチ喧嘩になりました。

アホです。

東大生なのに知性がないです笑。

　

今回は、

私が高1か高2くらいに発売されて、レベル的に使えなかった幻の参考書。そして、とてつもなくわかりやすいと噂で一度使ってみたかった

入門問題精講

を紹介します。

　

　

　

数学 入門問題精講
基本事項

↓が新学習指導要領版の入門問題精講です。

↓は現課程版なので気をつけてください。基本的に精講シリーズは色が濃くなるほど新しいです。（なんで濃いのかはわからないけど）

　

数学 入門問題精講
対象者

入門問題精講の対象者としては、

• 教科書がわからん
• 数学を０から学びたい
• 独学者/初学者
• 問題演習より講義型の説明を読みたい

という人におすすめ。

　

入門問題精講の「はじめに」にもありますが、

　

入門問題精講は、教科書の上位互換。よりわかりやすくした教科書。授業を活字化した参考書、と思ってもらえればいいです。

だから、

教科書の抽象的で固い説明に挫折した人も、学校の授業がわかりにくくてついていけなかった人も、単純に聞いてなかったけどやり直したい人も、使えます。

基本的に、

ほぼ初学者/独学者という人にピッタリ。

高校数学を０から一つずつ教えてくれます。

　

私の読者の方でも中１で進めることができている、という強者もいます。

入門問題精講神ですよ！私は中1で基礎問題精講進めてますが、映像授業も他の参考書も使わず入門問題精講だけでインプットしてます。

https://high-child.com/2024/02/08/うすっ！『文系の数学-重要事項完全習得編』のレ/
のコメント欄より

　

また、

問題演習を通じて新しいことを覚えていくというよりは、しっかりと解説を受けて知識をインプットし、それをアウトプットする形がいい、という人にもおすすめ。

単元ごとに重要事項やポイントの導入を最初にして、問題に入るので使いやすいと思います。

　

　

　

数学 入門問題精講
レベル

問題レベル：教科書ー入試基礎ー入試標準ー入試応用
前提レベル：０
到達レベル：共通テスト５〜６割

　

問題レベルについて。

入門問題精講に収録されている問題はすべて教科書レベルです。教科書の例題・練習問題レベルの問題がズラッと並び、一部章末問題レベルなので、入試レベル問題はありません。

入門問題精講の目的が問題演習ではなく、数学の理解・導入なので、そう考えたら問題は簡単なことに越したことはないでしょう。

　

前提レベルについて。

まったく必要ないです。強いていうなら、中学生レベルの数学は理解していてほしい。四則演算・展開・因数分解・三平方の定理くらいはわかっていてほしい。

ただどれも非常に詳細な説明が載っているので、不安に思う必要はありません。

　

到達レベルについて。

教科書レベルの勉強は終了します。

だから定期テストでは８〜９割近く取れるだろうし、共通テストでも５〜６割は取れるようになるでしょう。基礎問題精講や黄チャートに取り組めるレベルにもなります。

本格的に数学の受験勉強を始める準備が整います。

　

　

　

数学 入門問題精講
問題数

	練習問題	応用問題	合計
数学1A	95題	17題	112題
数学2B	116題	27題	143題
数学3C	107題*	18題*	125題*

※数学3Cのみ現行課程版の問題数です。

　

入門問題精講には例題は存在しないので、これで全部になります。

入門問題精講は総問題数が100~150題。

これは圧倒的に少ないです。

　

チャート式だと例題350題、練習問題350題、exercise・章末問題など300題くらいあるので、合計1000題あります。

基礎問題精講でさえ例題150、演習問題150ほどあるので合計300題です。

　

圧倒的な少数精鋭。

数学の今回を理解するために必要最低限な重要問題に絞ることで、非常に効率的に数学を理解できるシステムになっています。

無駄に難しい問題がないので、初学者でも挫折せずに無理なく進められる。

問題をこなすことに追われる必要がないので、理解に徹することができる。

　

このレベルとして最適な問題数だと思います。

　

　

　

数学 入門問題精講
内容

数学の入門問題精講は、

単元の中で、「講義」→「練習問題」→「精講」→「解答」→「コメント」のサイクルを繰り返します。１単元ごとに数問の「応用問題」もついています。

　

入門問題精講の一番秀逸な部分はこの「講義」の部分で、非常にわかりやすい。

知識０の人間でもわかるように解説されています。マジで、映像授業を活字化しただけです。実質、講義のまとめノートです。

百聞は一見に如かず。

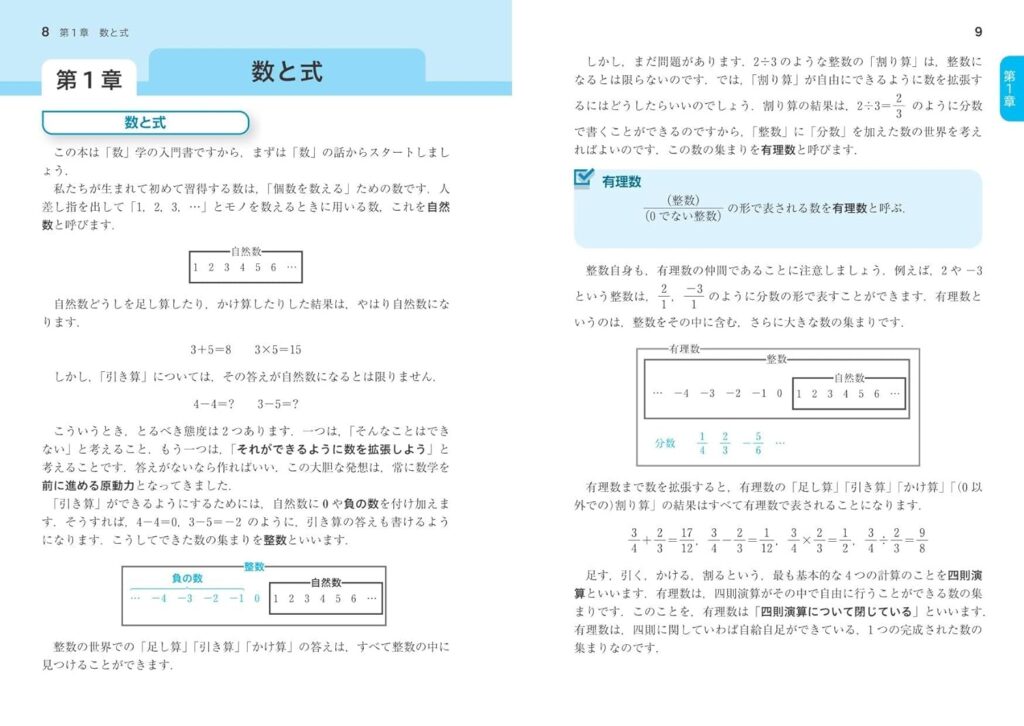
この「講義」によって、数学を体系的に学べます。問題演習ベースでインプットするよりも遥かに効率よく、高校数学を理解することができます。

　

そして、

「練習問題」のレベル設定もちょうどいい。

今「講義」で説明を受けたばかりの受験生が内容を理解していればギリギリ解けるくらいの問題レベルに設定されています。

「講義」の内容をそのまま写しても解けず、しっかり理解していないと解けないです。

内容理解の確認としてちょうどいいでしょう。

しかも、

これらの問題は後々分かりますが、入試基礎の典型・頻出問題につながってきます。学習効果の高い問題が選ばれています。

　

「精講」ではササっとポイントがまとめられており、ヒントのような使い方もできます。

また「解答」が非常に分かりやすい。

しっかり初学者を対象としていることを念頭に置いているので、　吹き出しで細かく式変形の意味を解説してくれます。

そのため初学者・独学者に起こりやすい「え、なんでこの変形するの？」という疑問を可能な限り解決してくれます。

最後に、

「コメント」で今回の問題を解く上でのポイントを再度まとめてくれます。

　

　

　

数学 入門問題精講
使い方

周回数：７周
ペース：4題/h×2周→12題/h×3周→20題/h×２周
やり方：
　単元ごとに4題/hで2周ずつ
→12題/hで全体を3周
→20題/hで全体を2周

	数学1A	数学2B	数学3C
問題数	112題	143題	125題
目安時間	100時間	125時間	110時間

　

「単元ごとに4題/hで2周ずつ」

1. 「講義」を熟読
   （7〜10分）
2. 「練習問題」を解く
   （〜3分）
3. 「精講」「解答」「コメント」を熟読
   （〜5分）

※講義で概念や公式を理解することを最優先にしてください。
※「練習問題」は解けそうなら３分を上限に解いてください。解けなさそうなら、即諦めて「解答」を読んでいいです。
※「解答」は解法を覚えるというより、吹き出しにも十分注意して、解法をしっかり理解することに集中しましょう。

　

「12題/hで全体を3周」

1. 「練習問題」を解く
   （1〜3分）
2. 「精講」「解答」「コメント」を熟読
   （0〜4分）
3. 適宜「講義」に戻ってもいい
   （0〜3分）

※解法を習得していくフェーズです。
※「練習問題」は１分悩んで手が動かなければ、「解答」へ。１分以内に解法が浮かべば解いてください。
※「練習問題」の正誤に関わらず「解答」は確認するように。無駄のない解法を覚えてください。
※解けるやつは1題2分とかで終わると思うので、悩んだり、不安なものは存分に「講義」で復習してください。

　

「20題/hで全体を2周」

1. 「練習問題」を解く
   （1〜3分）
2. 「精講」「解答」「コメント」を熟読
   （0〜4分）

※解法を定着・洗練させていくフェーズです。
※「練習問題」が○だった場合は「解答」等を読む必要はないです。
※１つ前の段階より瞬殺できる問題が増えてきていると思うので、平均1題3分でも進められるでしょう。

　

　

　

実際は、２周目・４〜５周目をもっと速く進められると思うので、頑張ってみてください。

　

　

　

数学 入門問題精講
接続

【大学受験】俺のガチおすすめ！数学の参考書ルートを紹介！

数学 入門問題精講
前の参考書

なし

　

スタディサプリを見るなら、入門問題精講をやる必要はないです。どちらかに絞りましょう。わからないところだけ映像授業を使用するのはアリですが。

　

　

　

数学 入門問題精講
次の参考書

• 基礎問題精講
• 黄チャート
• 文系の数学 重要事項完全習得編

　

個人的には基礎問題精講がおすすめ。

時間があるなら黄チャートでもいいと思います。（青チャートもギリ許容。）

入門問題精講があくまで数学の導入・理解のための参考書なので、網羅性が低く、入試の典型問題に触れられていません。

だから、

網羅系でしっかり典型・頻出問題の解法をおさえる勉強をしたいところです。

極めて残り時間が少なければ「文系の数学 重要事項習得編」とかでも可です。

数学は薄い問題集こそ正義！網羅系なのに薄い基礎問題精講とは？

うすっ！『文系の数学 重要事項完全習得編』のレベル＆使い方

　

　

　

まとめ

入門問題精講は神です。

これで、数学の導入は

スタディサプリor入門問題精講

となりました。

独学の方はぜひ自分に合った方を選んでみてください。