残すところ最後となりました「東大への道」シリーズ。
今回は「東大への道 数学編」ということで、やっていきたいと思います。
総論編は↓です。
ただ、数学編で語る内容は今までの「数学 勉強法」系の記事で話してきた内容と割とかぶるところがあります。購読者の方からすると少し面白みに欠けると思いますが、よろしくです。
目次
東大数学 対策

東大数学の基本情報
<基本情報>
配点:120点
時間:150分
<特徴>
- 6題すべて自由記述
- 初見の問題のみ
- 誘導は少ない
- 実は時間が不足する
まず常識ですが、東大数学は6問すべてが自由記述式となっています。どでかい空白が与えられて「どんなふうに記述してもいいよ」という解答形式。
多くの人は縦に2つに割って、左上→左下→右上→右下と進めていきます。
東大数学は厳密性重視なので、意外とあの空白をすべて文字で埋める勢いでOKです。よほど綺麗な解法を選ばない限り、余白が大幅に余るのは記述不足でしょう。
また東大数学の特徴として、初見の問題しか出ないこと。
パッと見で「あ、これ青チャートで見たことあるな」とは絶対にならないです。考察を重ねる中で、「これ一対一の例題の亜種と言えるのでは?」と気づく感じです。
しかもその上誘導は少ない。
たいてい小問が2~3つついています。(1)でかなり具体的な状況での理解を問う。(2)でより抽象どの高い状況でも(1)と似た考え方で考察する。
というパターンが多いです。
あと「6問を150分で解くなんて、絶対時間余るやん!」と初めての人は思いがちですが、全くそんなことないです。
150分なんてあっという間に過ぎます。
どの問題もノンストップで解いて、丁度150分で6問解き終わるくらいなので、そこは勘違いのないようにしたいです。
東大数学の傾向
直近10年分の出題傾向のまとめです。数字は大問を表してます。融合問題は複数分野にわたって大問番号を書いているので、出題率の合計は100%を超えます。
文字:出題率10%〜
文字:出題率5%〜
| 分野 | 出題率 | 2023 | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 |
| 整式系 | 6.7% | 5 | 6 | 1 | 6 | ||||||
| 図形と計量 図形の性質 空間図形 | 5% | 2 | 2,3 | ||||||||
| 二次関数 | 5% | 3 | 1,5 | ||||||||
| 場合の数・確率 | 10% | 2 | 6 | 2 | 2 | 2 | 2 | ||||
| 整数 | 15% | 2 | 4,6 | 4 | 4 | 4 | 5 | 5 | 5 | ||
| 図形と方程式 (軌跡・領域) | 11.1% | 3 | 1 | 5 | 3,5 | 1 | 6 | ||||
| 指数・対数・三角関数 | 3.3% | 1 | 1 | ||||||||
| 微分・積分 微分法・積分法 立体の求積 | 40% | 1,3,6 | 1,4,5 | 3,5 | 3,5 | 1,2,5 | 1,4,6 | 5,6 | 1,3,6 | 3,6 | 3 |
| 数列 (主に漸化式) | 16.7% | 2 | 4 | 5 | 2 | 4 | 2,4 | 2,4,5 | |||
| ベクトル | 5% | 4 | 3 | 1 | |||||||
| 複素数平面 | 8.3% | 2 | 6 | 5 | 3 | 4 | |||||
| 二次曲線 | 1.7% | 6 | |||||||||
| 極限 | 5% | 1 | 5 | 4 |
東大数学の頻出分野としては、
- (確率)
- 整数
- 軌跡領域
- 微分・積分(立体の体積)
- 数列
あたりが挙げられます。
確率は2017年くらいまで超頻出分野で、出題されると必ず確率漸化式を立てて解くだけの、サービス問題でした。
しかし2022年に5年ぶりの出題では、ゴリゴリに難しい捨て問としての出題でした。
おそらく、東大側からのメッセージで、「もうあんな簡単な確率は当分出さないよ」ということでしょう。
なので、今後でる可能性はそんな高くないと予想しての()です。
整数もたびたび出題されますが、絶対解けない難問と、ちょっと工夫すれば解けるやや易問題の2種類出ます。
どちらかすぐ判断して解くのが大事。
難問のときは物凄い沼るので。
軌跡領域・通過領域は本当に頻出で、標準~やや難であることが多いです。
2022年は領域が2問出てます。片方はやや易か標準くらい。もう一方はやや難~難って感じです。
微分・積分は高校数学の集大成なので必ず出ます。
単純な計算力が問われるような問題を割と出題しがちで、思考力自体は要求されないのでサービス問題。計算さえ合わせれば勝ちです。
逆に計算力1つで差がついてしまうので、ここはミッチリ対策してください。
回転体の体積なんかも頻出。
切り方・計算の仕方は要復習です。
数列は基本的に、確率漸化式や極限、整数などと絡めた出題が多く、単体での出題はほぼないです。
数列自体を重点的に対策する必要はないですが、基本的な数列の解法などには慣れておいてくださいって感じです。
あと最近の流行りとしては、
- 複素数平面
- 整式系
最近確率に代わって頻出なのは複素数平面。2016年以降の出題が目立ちます。図形的考察と絡めたり、軌跡と絡んだりします。
複素数の扱いには慣れておきましょう。
また昔も出てましたが、整式の論証系の問題がちょくちょく出ます。
指導要領的にはそんな範囲は存在してないですが、難しい参考書を進めていけば必ず載っている問題なので、是非とも慣れておいてください。
東大数学の目標点
得意な人:75点
目安目標:60点
苦手な人:45点
<合格者平均点の観点>
2022年以降と、2021年以前で難易度に大きな差があるので単純に絶対指標としての目標点の考察には、2022・2023年のみで行います。
| 合格者平均点 | 2022年 | 2023年 |
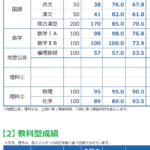
| 理科1類 | 61.2 | 53.6 |
| 理科2類 | 53.3 | 54.9 |
| 理科3類 | 76.2 | 71.3 |
やっぱり合格者平均点的には、理科1類で60点、理科2類で55点、理科3類で75点とれればよいでしょう。
そう考えれば、
目標得点は60点が妥当だと思います。
60点以上とれれば基本的にはアドになります。45点を下回ると、合格者たちと大きく差をつけられてしまうので避けたいところ。
苦手な人も死ぬ気で45点は確保したい。
<問題レベルの観点>
目安目標を取る例として、「3完」or「2完2半」or「1完4半」です。
東大理系数学の出題として、大学への数学評価で
B問題:1題
C-問題:1題
C問題:2題
C+問題:1題
D問題:1題
くらいを目安に出題されます。
C+やD問題だとそもそも(1)から難しいので、半完するのも難しいでしょう。
そう考えると現実的には「3完」か「2完2半」が妥当です。
だから
まず何とかB,C-問題を2題探してきて、完答するところから始まります。
目利きの能力が大事。
あとは残る4題の中からC問題など手を出せそうな問題の(2)の初めの方まで解ければ勝ち。
数学が苦手な人なら、1完3半が狙い。
B問題は仕留めて、あとはC問題3つの(1)だけ完璧に合わせる。
それで45点以上です。
東大数学の途中点は?
東大数学の中でも肝になるのが、
いかに途中点を集めるか
勉強し始めの頃は誰でも「4完してやる!」と意気込むんですが、結局完答の難しさに阻まれます。
そこで大事になってくるのが、いかにして途中点を集めるか。
逆に答えだけあっていても論理性を欠く答案なら、問答無用で大幅減点を食らいます。
https://todai.info/juken/data/2022/kaiji_4.php#mathS
- 3冠半行けたはず……と思っていたら、論理の矛盾を突かれて大幅に減点されていた。
考える癖、数学的思考が完成されていないことが問題だと思われた。- 模範解答に対する進捗度合いに応じてそのまま点数が入ってる印象。計算ミスするとそこから下に点は入らないし、方針が脱線しても点は入らない
- 計算ミスなど凡ミスには相当優しい
恐らく2〜3点くらいしか引いていない- 思ったより厳しい。
駿台の方が採点近い。- 過程, 論理が合っていて最後まで答案を書き切っているが途中に軽微な計算間違いなどのミスがある答案に(最終的な答えが合ってなくても)かなり点が来た印象
実際の受験者の声としてはこんな感じです。
東大数学の途中点を集める上で大事なのは、
「論理的整合性」
になります。
- 同値変形か十分条件か必要条件か
- 数式操作の説明があるか
- 方針の見通しが良いか
特に式変形にはこだわりましょう。
√ を2乗したら、それは本当に同値なのか。同値なら、どんな条件の元、同値と言い切れるのか。根拠はどこから拾ったのか。
十分条件なら、そう言って式を書きましょう。
東大は式変形には非常に厳しいので、そこら辺を曖昧にやり過ごそうとすると大幅な減点を食らう可能性が出てきます。
また大事なのは採点官に、自分の方針をわかりやすく伝えること。
どんな解法・操作を行うか、どの視点から問題を解いていくか。それをハッキリするだけでも、途中点が入る可能性は十分ありますし、自分の思考整理にもなります。
東工大の話ですが、
昔超難問が出た時に「数学的帰納法により示す」と書いただけで10点近くの途中点が入ったという、有名な話があります。
しっかり見通しよく、わかりやすく、論理的な答案を書く練習をしましょう。
東大数学の勉強法
東大数学へ向けて
東大数学で十分な点数を取る上で大事なことは、
- 典型パターンの解法習得
- 初見の問題へのアプローチ
の2つの勉強をしていくことです。
まず天下の東大数学といえど、まったく新出の問題を出すわけではないです。
元となる考え方や典型問題を少しイジったり、融合させた問題を出題する場合がほとんどであることは、周知の事実です。
なんならほぼ典型問題通りの問題が出ることもあります。
だから第一に典型パターンの解法を習得していることが大前提になります。
詳しい話は↓でしているのでぜひ。
この習得というのも、どの解法を使うかわかれば、あとは自動化されるようなレベルでないとダメです。
東大数学はそうでなくても量が多く、思考のキャパも、処理のキャパも圧迫されます。
そこで典型パターンを処理するのに、脳のキャパも時間的キャパも使っていれば、当然他の受験生には差をつけられます。
青チャートの例題や基礎問題精講などの典型パターン習得は、死ぬ気でやりましょう。
そして、次はアウトプットの練習です。
さんざん習得した解法のうちどれが有効で適用できるのか。その方針を見抜く力が東大数学では非常に大事になってきます。
初見の問題に対して、どこからアプローチしていくか。
どの典型パターンに帰着させるか。
それを見抜く練習は間違いなく必要です。
東大数学の対策 参考書
<45点を目指す>
「基礎問題精講」
or
「黄/青チャートの例題」
+
「一対一対応の演習」
or
「標準問題精講」
+
「過去問」
典型パターンの習得にすべてを注ぎます。
入試本番では、本当に典型パターンに似ているものを1,2題完答するだけ。残りはひたすら(1)を集める。
それでも45点は可能なので、頑張りようはいくらでもあります。
<60点を目指す>
「基礎問題精講」
or
「黄/青チャートの例題」
+
「一対一対応の演習」
or
「標準問題精講」
+
「プラチカ」
or
「新数学スタンダード演習」
or
「やさしい理系数学」
+
「過去問」
「プラチカ」「新数学スタンダード演習」「やさしい理系数学」の中からは何冊やってもいいです。
ただおすすめは「プラチカ」「新数学スタンダード演習」です。
「やさしい理系数学」は問題の文字や設定が綺麗すぎて、定理や性質の証明問題集みたいになっています。本番ではもっと泥臭い問題が出るのに。
その点再現ができていないので、あまり演習教材としては良くないでしょう。
<75点を目指す>
「基礎問題精講」
or
「黄/青チャートの例題」
+
「一対一対応の演習」
or
「標準問題精講」
+
「プラチカ」
or
「新数学スタンダード演習」
or
「やさしい理系数学」
+
「新数学演習」
or
「上級問題精講」
or
「ハイレベル理系数学」
+
「過去問」
「入試数学の掌握」
ここまでくるとどれだけ演習してもいいです。
特に「新数学演習」と「上級問題精講」は、東大入試本番とほとんどレベル感が一致しているので、非常に良い演習になると思います。
「ハイレベル理系数学」は相変わらず好きじゃないです。
で、過去問とは違いますけど「入試数学の掌握」もおすすめ。
こちらは方針の立て方に全振りした参考書です。初学者が見てもなんの意味もないですが、一通りすべての勉強を終えた人が使うと非常に強いです。
数学に対する新しい視点がひらけます。
時間が許すならぜひやりたいところ。
<過去問系の参考書紹介>
過去問系として、
- 赤本27ヶ年
- 青本25ヶ年
- 鉄緑会10年
- 鉄緑会30年
- 実戦/オープンの過去問
- 東大数学で1点でも多く取る方法
ここら辺ですね。
「赤本」と「青本」は無難におすすめ。
収録年数も多く、解答も普通に作られてます。ただ解説や方針が多少雑なのと、採点基準がついていないので、本当に文字通り過去問演習って感じになります。
「鉄緑会の過去問」は強いです。
方針の立て方や、別解、採点基準、レベル感などなど基本的に思いつく限りのことが載っています。
ただ情報量が多過ぎて、すべて吸収するとなると膨大な時間を要します。そのため、取捨選択しつつ演習するか、大量の時間をかけてやり込むかになります。
少々癖の強い過去問です。
「実戦/オープンの過去問」はやること無くなった人向け。
実戦≧本番>>オープンくらいの難易度です。まあ買うなら実戦の過去問かなって感じです。当時の平均点や偏差値表もあるので、いい刺激にはなると思います。
参考書についてはこっちを参照してください。
まとめ
「東大への道」シリーズはこれで完結です。「共通テスト編」は流石にいらないでしょう。
東大入試に対する対策は知る限り書いたと思います。
あとは勉強するだけです。
頑張ってください。
「総論編」から各科目に飛べます。








コメント失礼します
1対1対応の演習1a2b3cを6ヶ月程かけて習得しようと思うのですが、1冊ずつ周回するか、6冊一気に周回するかどちらが良いと思いますか?
私は絶対的に一冊ずつがいいと思います。
東大理二志望の高2です。
現在一対一を進めているのですが、数Aの図形の性質もやるべきでしょうか。
ある程度はチャートで解いている為共テの図形の性質の問題はほぼほぼ解けます。
じゃあ、時間がなければやらなくてもいいでしょう。
返信ありがとうございます。
一旦図形の性質はスキップして必要を感じたらやろうと思います。
ブログの記事、とても参考になっております。
有難う御座います!
ブログの記事には記述が未だ無いですが、
ハイレベル 数学i・A・Ii・B の完全攻略はどうでしょうか?
販売先のコメント欄には大変良いとか最強とか評価する人が多く、非常に気になっております。。
宜しくお願い致します。
私がそれを使ってなかったので、あんまり書く気が起きないっていう感じです。今度書きます
お待ちしております!
こんにちは。
現在中2、中学受験偏差値55くらいの中高一貫校に通っています。
数学がとことん苦手で、この前駿台の中3の模試を受けたら40点/100点満点 でした。
でも東大の理3にどうしても入りたいです。
学校はもう数1.Aに入っていますが、青チャートと中心なのに定期で6割くらいしか取れていません。
そこで質問です。
スタサプで中学総復習
↓
スタンダード
↓
ハイレベル
そこまで済んだら
青チャートの例題
と進んでいくつもりなのですが、それで大丈夫ですか?
教えていただけると嬉しいです。
ハイレベルはいらないと思います。他はよいです。
ありがとうございます。
ハイレベルは抜くことにします。
文三志望の高2です。数弱で基礎を叩き込もうとずっと青チャートをやっていたのですが分厚いのは効率が悪いと言われて文系数学実践力向上編に変えました。プラチカに接続しようと思ってます。青チャート→一対一→プラチカルートと現在のルートどちらが効果的でしょうか。また青チャートに戻すとしていつまでに完成していればいいでしょうか。
どちらでも大差ないです。ただ、他人に少し言われただけで青チャートを止めてしまったのは勿体ない気もします。受験の基本は一冊を完璧に。それだけ忘れなければ、どちらのルートも問題ないと思います。
正直チャートに未練ありまくりです。数学がスランプになってしまった時に少し間を置いてチャートをやったらなかなか力が入り切らず、嫌になったのもあって変えてしまいました。行き詰まったらチャートに帰ろうと思います。
こんにちは。理一志望の高2です。記事内では最後に掌握がおすすめされておりますが、新スタの後にやるのは効果的でしょうか。
十分効果はあると思います